Área do cubo

A área é a medida da superfície de uma figura ou sólido geométrico. O seu cálculo é feito por meio de algumas fórmulas simples, mas diferentes para cada sólido ou figura geométrica. Desse modo, existe uma expressão matemática específica para o cálculo da área do cubo.
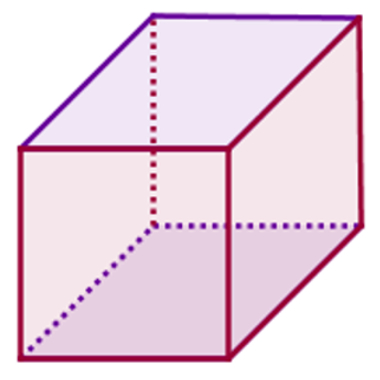
Imagem de um cubo ou hexaedro regular
O cubo é um poliedro regular que possui seis faces quadradas. Dessa maneira, todas as arestas do cubo são congruentes.
Quando se trata de sólidos geométricos, existem algumas possibilidades de cálculo de área: área da base, área lateral e área total. Geralmente, a área total é a soma das áreas das bases e a área lateral.
Área da base
Os cubos são poliedros classificados como prismas. Esses poliedros possuem duas bases congruentes. Desse modo, sabendo que todas as bases do cubo são quadrados, podemos afirmar que as suas duas bases são quadrados congruentes e, por isso, possuem a mesma área.
A fórmula para calcular a área de uma das bases do cubo é a mesma usada para a área do quadrado:
Ab = l2
“l” é o lado do quadrado ou a aresta do cubo.
Área lateral
A área lateral de um prisma é dada pela soma das áreas das faces laterais (face lateral é qualquer face que não é base). Para facilitar a visualização, observe a planificação do cubo da imagem anterior na imagem seguinte:
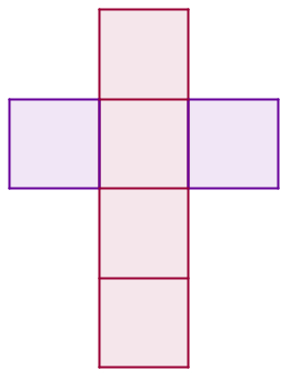
Note que as bases foram colocadas lateralmente, e as quatro faces laterais ficaram na coluna central. Observe também que as faces laterais de um cubo também são quadrados congruentes às bases. Dessa maneira, tendo em vista que as arestas desse poliedro medem l, a fórmula para calcular uma face lateral é a seguinte:
Afl = l2
A área lateral será a área de uma face lateral multiplicada por quatro:
Al = 4·l2
Isso é o mesmo que somar as quatro faces laterais do cubo.
Área total
A área total de um prisma é dada pela soma das áreas laterais e das bases. Como o cubo possui duas bases, para calcular sua área total, devemos proceder conforme a seguinte expressão:
At = Al + Ab + Ab
E isso é equivalente a:
At = Al + 2·Ab
Tendo em vista que todas as áreas laterais e das bases de um cubo são iguais e escrevendo a fórmula acima e a função da área da base, podemos afirmar que a área de um cubo é:
A = 6·Ab
Exemplos
1º) Um artista plástico foi convidado a pintar uma escultura na forma de dado que seria doada posteriormente para uma cidade A. Essa escultura possui formato de cubo e aresta com 2 m. A face 1 desse cubo deve ficar voltada para o chão, fazendo com ele um ângulo de 15° e estando suspensa a 2,5 m de altura. Essa face deve ser pintada de vermelho, assim como a oposta a ela. As outras devem ser pintadas em azul.
a) Supondo que uma lata pequena de tinta seja suficiente para pintar 2 m2 do cubo, quantas dessas latas serão usadas para pintar a sua parte vermelha?
Solução: Podemos tomar a parte vermelha do cubo como suas bases. Para calcular a área delas, podemos usar a fórmula:
Ab = l2
Substituindo o valor da aresta, teremos:
Ab = 22
Ab = 4
Desse modo, uma das bases mede 4 m2. As duas juntas, portanto, medem 8 m2. Para pintá-las, serão usadas quatro latas de tinta.
b) Supondo que uma lata pequena de tinta seja suficiente para pintar 2 m2 do cubo, quantas dessas latas serão usadas para pintar a sua parte azul?
Solução: A área em azul representa a área lateral do cubo e pode ser calculada da seguinte maneira:
Al = 4·l2
Al = 4·22
Al = 4·4
Al = 16
O cubo possui 16 m2 de área lateral e, portanto, serão usadas oito latas de tinta para pintá-la.
c) Qual é a área total do cubo?
Solução: Basta utilizar a fórmula dada anteriormente para calcular a área do cubo.
A = 6·Ab
A = 6·4
A = 24 m2
Artigos Relacionados

Últimas notícias
Outras matérias


















