Ângulos alternos internos e externos
Ângulo é a medida da abertura entre duas semirretas. Essa medida também pode ser observada entre retas, entretanto, a intersecção entre duas retas gera quatro ângulos em vez de um só. Quando duas retas paralelas são cortadas por uma reta transversal, são formados oito ângulos que possuem propriedades e características comuns à posição que ocupam.
Retas paralelas – região interna e externa
Duas retas r e s são chamadas de paralelas quando não possuem nenhum ponto em comum. Para representar o paralelismo, podemos escrever apenas: r\\s.
A região que fica entre as duas retas paralelas, colorida na figura abaixo, é a região interna dessas duas retas.

Região interna das retas paralelas r e s
Já a região que não fica entre as duas retas é chamada de região externa. Observe na imagem a seguir todos os ângulos formados por uma retra transversal a r\\s e que estão na região externa dessas retas.

Ângulos alternos internos
O nome já indica a posição ocupada por ângulos alternos internos. A palavra interno indica que esses ângulos estão na região interna das retas paralelas, e a palavra alterno indica que eles estão em posições alternadas com relação à reta transversal. Sendo assim, ângulos alternos internos são aqueles que estão na região interna das retas paralelas e em lados alternados da reta transversal.
Observe na figura a seguir que os ângulos α e β estão na região interna das retas r e s. Ao mesmo tempo, o ângulo α está à direita e o ângulo β está à esquerda da reta transversal.
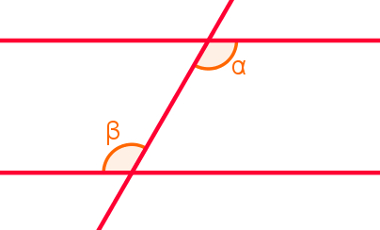
Assim, podemos dizer que α e β são alternos internos.
Ângulos alternos externos
Ocupam a região externa das retas paralelas e, ao mesmo tempo, estão em lados opostos da reta transversal. Observe um exemplo de ângulos alternos externos na figura a seguir.
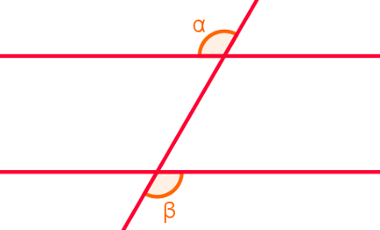
É válido destacar que os ângulos alternos externos e internos são congruentes.
Exemplos
Calcule a medida dos ângulos em destaque na figura a seguir.
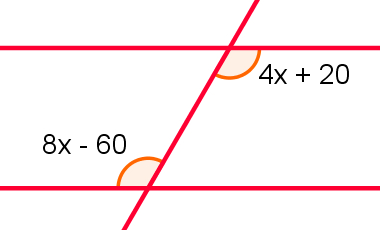
Solução:
Sabendo que ângulos alternos internos são iguais, podemos escrever a seguinte equação:
8x – 60 = 4x + 20
8x – 4x = 20 + 60
4x = 80
x = 80
4
x = 20
Para calcular os valores dos ângulos, basta substituir x na expressão dada para cada um deles. Observe:
8x – 60 =
8·20 – 60 =
160 – 60 =
100°
4x + 20 =
4·20 + 20 =
80 + 20 =
100°

