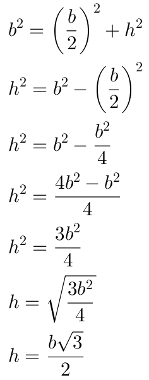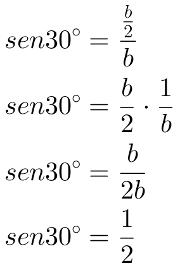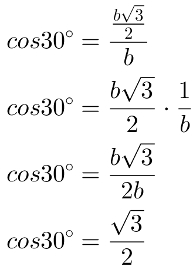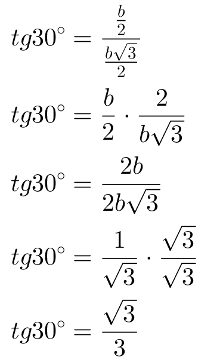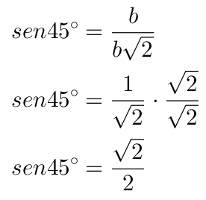Ângulos notáveis

Ângulos notáveis são assim conhecidos em razão de sua importância para a Geometria. Eles são provenientes da Trigonometria, conteúdo em que se destacaram como os mais comuns e por apresentarem resultados diferenciados em seus cálculos. Os ângulos notáveis são: 30°, 45° e 60°.
Além desses, vale fazer uma “menção honrosa” aos ângulos 0°, 90° e 180°. Entretanto, não é possível utilizar as razões trigonométricas para esses ângulos na trigonometria básica.
Para cada ângulo, existe um valor de seno, cosseno e tangente, mas os valores encontrados para os ângulos notáveis podem ser expressos de maneira vantajosa. Adiante, veja uma tabela contendo todos os valores de seno, cosseno e tangente desses ângulos.
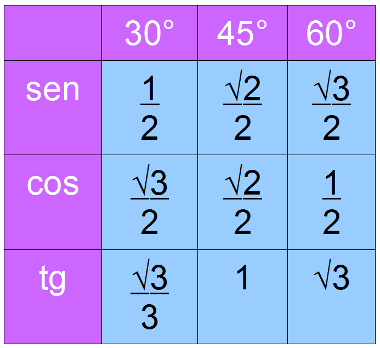
Tabela de valores para ângulos notáveis
Independentemente das medidas dos lados do triângulo, se ele for retângulo, e um dos outros dois ângulos tiver uma das medidas na tabela abaixo, seno, cosseno e tangente desse ângulo serão:
Lembrando que os valores das tangentes desses ângulos podem ser obtidos dividindo os valores do seno pelo cosseno, desde que eles pertençam ao mesmo ângulo.
Demonstração dos valores de seno, cosseno e tangente
Os valores dados na tabela anterior são válidos para qualquer triângulo retângulo que possua um ângulo de 30°, 45° ou 60°. Para encontrar esses valores, precisaremos de um triângulo retângulo que possua esses ângulos e das medidas de seus lados.
Para construir um triângulo com esses ângulos, conhecendo suas medidas, vamos tomar como ponto de partida um triângulo equilátero ABC, cujos lados medem b. Observe que cada um dos ângulos internos de um triângulo equilátero mede 60°, pois eles são todos iguais e a soma deles deve totalizar 180°.
Partindo do vértice B, construiremos a altura que vai até o lado AC, tocando-o no ponto D. Essa altura é também mediana do lado AC e bissetriz do ângulo B, pois essa é uma das propriedades da altura, mediana e bissetriz de triângulos equiláteros. Sendo assim, teremos a seguinte construção:
Observe que, por ser bissetriz e mediana, o segmento BD divide o ângulo B em outros dois ângulos de 30°, e o segmento AC em outros dois segmentos com medida igual a b/2.
Agora, considere apenas o triângulo retângulo BCD, extraído do triângulo equilátero da imagem acima. Nesse triângulo BCD, ilustrado na imagem a seguir, será possível calcular o seno, o cosseno e a tangente dos ângulos de 30° e 60°.
Para isso, porém, será necessário calcular a altura h desse triângulo em função de b. Nesse caso, usaremos o teorema de Pitágoras:
Com a obtenção dessa medida, podemos calcular as razões trigonométricas uma a uma, considerando, para isso, o mesmo triângulo BCD. Assim, é preciso lembrar das definições dessas razões, que podem ser encontradas clicando aqui.
Sen30°:
Cos30°:
Tg30°:
Para encontrar os valores referentes a seno, cosseno e tangente de 60°, devem ser feitos cálculos análogos (equivalentes) a esses, porém, considerando o ângulo de 60°.
Antes de passar para os valores de seno, cosseno e tangente de 45°, será necessário construir uma outra figura.
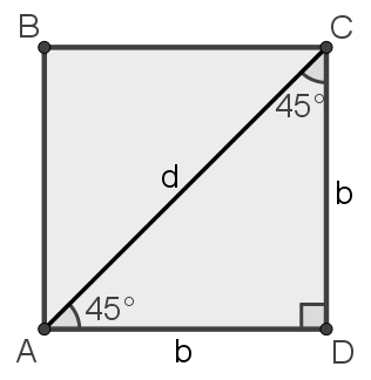
Considere um quadrado ABCD de lado b, trace sua diagonal AC. Observe que, como o quadrado possui todos os lados iguais e, considerando apenas o triângulo ACD, teremos as seguintes medidas:
Além disso, considerando o triângulo ACD isósceles, pois possui dois lados iguais, os ângulos da base devem ser congruentes. Como um dos ângulos desse triângulo mede 90°, os ângulos da base devem medir 45° cada.
Assim, fica fácil pensar em usar esse triângulo para calcular seno, cosseno e tangente de 45°. Antes disso, será necessário calcular a medida da diagonal do quadrado em função de b, também pelo teorema de Pitágoras:
d2 = b2 + b2
d2 = 2b2
d = √2b2
d = b√2
De maneira análoga a que foi feita anteriormente, observe:
sen45°:
Para realizar os cálculos relacionados às razões cosseno e tangente de 45°, também são seguidas, portanto, formas semelhantes a essa.
Artigos Relacionados

Últimas notícias
Outras matérias







.jpg)
.jpg)