Área do círculo
Para compreendermos a fórmula utilizada no cálculo da área de um círculo temos que imaginar uma circunferência:
E dentro dela circunscrito um polígono regular:
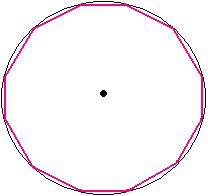
Os seguimentos de reta que partem do centro da circunferência e que vão até o vértice do polígono regular são os raios do círculo. Assim, formando n triângulos no polígono regular, com base no cálculo da área de um hexágono regular, podemos dizer que a área de um polígono regular de n lados seria:

A = n . a . h
2
Sendo n . a o valor do perímetro do polígono regular
A = (perímetro do polígono regular) . h
2
Agora imagine se aumentarmos o número de lados do polígono regular, a tendência é do seu perímetro ficar cada vez mais parecido com o comprimento da circunferência, e a altura de cada triângulo formado no polígono regular ficar igual ao raio do círculo. Assim, podemos concluir que a fórmula do cálculo da área de um círculo poderá ser indicada da mesma forma que a área de um polígono regular de n lados, veja a relação abaixo:
A = (comprimento da circunferência) . raio
2
A = 2πr . r
2
A = π r2
E dentro dela circunscrito um polígono regular:
Os seguimentos de reta que partem do centro da circunferência e que vão até o vértice do polígono regular são os raios do círculo. Assim, formando n triângulos no polígono regular, com base no cálculo da área de um hexágono regular, podemos dizer que a área de um polígono regular de n lados seria:
A = n . a . h
2
Sendo n . a o valor do perímetro do polígono regular
A = (perímetro do polígono regular) . h
2
Agora imagine se aumentarmos o número de lados do polígono regular, a tendência é do seu perímetro ficar cada vez mais parecido com o comprimento da circunferência, e a altura de cada triângulo formado no polígono regular ficar igual ao raio do círculo. Assim, podemos concluir que a fórmula do cálculo da área de um círculo poderá ser indicada da mesma forma que a área de um polígono regular de n lados, veja a relação abaixo:
A = (comprimento da circunferência) . raio
2
A = 2πr . r
2
A = π r2
Publicado por Danielle de Miranda
Assista às nossas videoaulas
Artigos Relacionados
Área da Coroa do Círculo
Clique aqui e aprenda como encontrar a área da coroa do círculo.
Área do Segmento Circular
Segmento de um Círculo.
Área do trapézio
Aprenda a calcular a área de um trapézio. Conheça a fórmula para calcular a área desse polígono. Saiba classificar o trapézio como isósceles, escaleno ou retângulo.

Matemática do Zero
Matemática do Zero | Soma dos ângulos externos de um polígono convexo
Nessa aula demonstrarei a fórmula da soma dos ângulos externos de um polígono convexo qualquer e como encontrar a medida de cada ângulo externo.
Últimas notícias
Outras matérias
Biologia
Matemática
Geografia
Física
Vídeos

Saúde e bem-estar
Leptospirose
Foco de enchentes pode causar a doença. Assista à videoaula e entenda!

Gramática
Inglês
Que tal conhecer os três verbos mais usados na língua inglesa?

Matemática
Regra de três
Com essa aula você revisará tudo sobre a regra de três simples.















