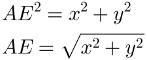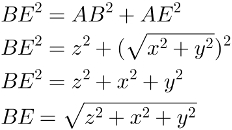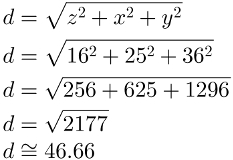Diagonal do bloco retangular

A diagonal de um polígono é um segmento de reta que liga dois de seus vértices e não é um de seus lados. A diagonal de um poliedro é um segmento de reta que liga dois de seus vértices não pertencentes a uma mesma face. Essa última também é a definição da diagonal do bloco retangular, já que ele é um poliedro.

Existe uma fórmula que pode ser usada para encontrar o comprimento da diagonal do bloco retangular. Ela é encontrada pelo Teorema de Pitágoras em um bloco de dimensões quaisquer, ou seja, representadas por letras. O uso desse teorema só é possível porque todas as arestas adjacentes de um bloco retangular são perpendiculares.

Diagonal do bloco retangular

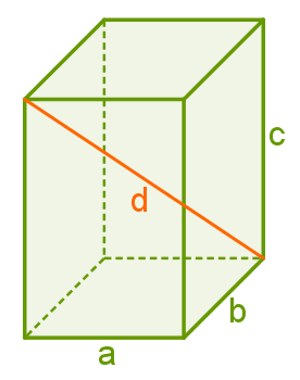
A figura a seguir representa um bloco retangular cujas dimensões são a, b e c e cuja diagonal é d.

Tendo em vista esse bloco retangular, o comprimento de sua diagonal (d) é obtido pela fórmula:

Nesse caso, a pode ser compreendido como largura; b, como comprimento, e c, como altura do bloco.

Teorema de Pitágoras e o bloco retangular

Para chegar à fórmula acima, é preciso usar o Teorema de Pitágoras. Para tanto, é necessário construir dois triângulos retângulos no bloco retangular.

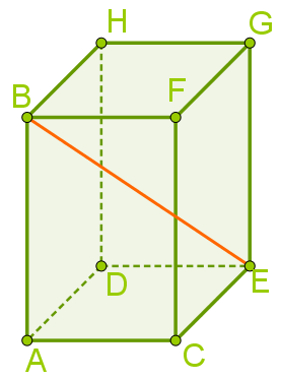
Observe o bloco retangular ABCDEFGH abaixo:

As medidas desse bloco retangular são: largura (AC) igual a x, comprimento (CE) igual a y e altura (EG) igual a z.

Note que qualquer segmento de reta que passe por A e pertença à base inferior ACDE é perpendicular ao segmento AB. Assim sendo, o segmento AE formará um ângulo reto com AB e, assim, poderemos observar o triângulo retângulo ABE.

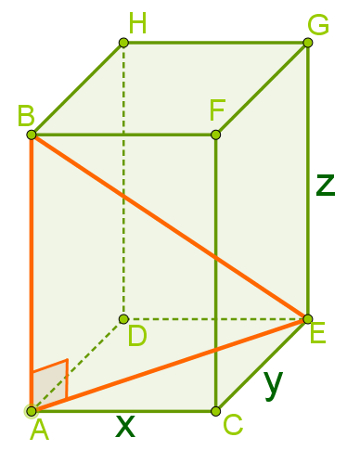
Triângulo retângulo observado no bloco retangular

Perceba que o segmento BE é, ao mesmo tempo, diagonal do bloco retangular e hipotenusa do triângulo retângulo construído. Os segmentos AB e AE são catetos desse triângulo.

Assim, para descobrir a medida da diagonal BE, basta usar o Teorema de Pitágoras para descobrir a medida dessa hipotenusa. Entretanto, conhecemos apenas a medida de um dos catetos: AB = z. Para descobrir a medida do cateto AE, usaremos também o Teorema de Pitágoras.

Para isso, observe que o segmento AE é hipotenusa do triângulo retângulo ACE. O ângulo C é reto, pois todas as faces de um bloco retangular são retângulos. A partir das medidas x e y dos catetos desse triângulo, descobriremos a medida AE que ainda falta:

A partir da medida de AE, usaremos novamente o Teorema de Pitágoras:

Exemplo

As dimensões de um bloco retangular são: 16 metros de largura x 25 metros de comprimento x 36 metros de altura. Qual a medida da diagonal desse bloco retangular?

Solução:

Usando a fórmula referida anteriormente, teremos os seguintes cálculos:

Também é possível usar apenas o Teorema de Pitágoras para resolver esse exercício. Basta repetir todo o processo usado para encontrar a fórmula trocando as letras x, y e z pelos seus respectivos valores.