Dimensões do espaço

Cada dimensão que um espaço possui está relacionada com a possibilidade de obter medidas de distância dentro daquele espaço. Se desenharmos um quadrado em uma folha de papel, por exemplo, será possível medir sua largura e altura, mas não será possível determinar a profundidade, pois o quadrado está limitado à folha de papel (o espaço) que o contém.
Uma dimensão
Existem espaços e objetos que possuem apenas uma dimensão. Isso significa que, dentro desses espaços, é possível calcular apenas uma única medida. Essa medida pode ser uma altura, uma largura ou um comprimento, mas sempre será apenas uma dessas três.
As “figuras geométricas” mais comuns que possuem apenas uma dimensão são as três seguintes:
Observe que é possível tomar uma única medida a partir de segmentos de reta: a distância entre seus pontos extremos. Essas figuras não possuem largura ou profundidade. Além disso, as retas podem ser consideradas como um espaço unidimensional. Isso significa que, dentro delas, é possível “desenhar” figuras que possuem uma dimensão.

Segmento de reta desenhado em um espaço unidimensional, ou seja, em uma reta
Duas dimensões
Um exemplo de figura que depende de uma segunda dimensão para ser desenhada é o quadrado. Note que seus contornos são formados por segmentos de reta, mas que existe um ângulo entre esses segmentos, o que faz com que alguns deles não possam ser desenhados por meio apenas do espaço unidimensional. Veja a figura a seguir:
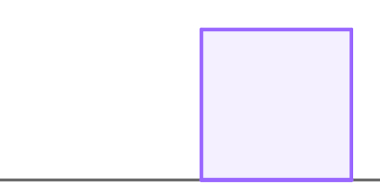
Sendo assim, fica definido que figuras bidimensionais são aquelas em que é possível medir comprimento e largura. São exemplos dessas figuras: quadrados, círculos, retângulos etc. Perceba que todas essas figuras são planas, pois o espaço usado para desenhá-las é plano. Dessa maneira, fica definido que plano é o espaço bidimensional onde é possível medir o comprimento e a largura das figuras.
Note também que largura e comprimento são duas medidas perpendiculares.
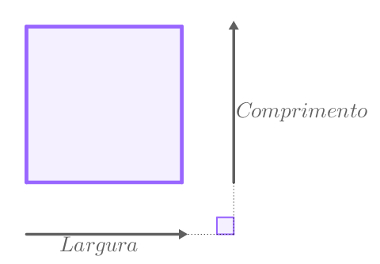
Três dimensões
A figura a seguir mostra um quadrado em perspectiva sobre um plano disposto horizontalmente. Note que a medida da diagonal do quadrado está sobre ele e, mesmo assim, não define outra dimensão. Ao lado do quadrado, foi construído um cubo sobre o mesmo plano. A medida que precisamos para definir a terceira dimensão está relacionada com a altura desse cubo, também chamada de profundidade, e é ortogonal à largura e comprimento.
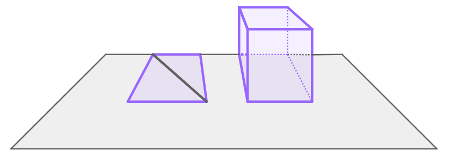
Objetos tridimensionais, portanto, são aqueles em que é possível medir comprimento, largura e altura (ou profundidade). São exemplos desses objetos os cubos, pirâmides, prismas, cones, cilindros etc.
O espaço tridimensional também é chamado apenas de espaço. Ele é justamente o espaço que nos rodeia. Assim, somos mais acostumados com objetos tridimensionais do que com qualquer outra figura geométrica.
Quatro dimensões
Note que não é possível encontrar qualquer segmento de reta que seja ortogonal à largura, comprimento e altura dentro do espaço onde vivemos. Qualquer segmento de reta imaginável pertencerá a esse espaço tridimensional. Assim, para definir a quarta dimensão, imaginamos uma quarta medida intimamente ligada às outras três que representa a linha do tempo. Os sentidos humanos não são capazes de perceber outras dimensões, embora elas existam matematicamente.
Artigos Relacionados

Últimas notícias
Outras matérias


















