Inequação exponencial
A inequação exponencial é uma sentença matemática que possui, pelo menos, uma incógnita em seu expoente e uma desigualdade. Encontrar o conjunto de soluções de uma inequação exponencial é encontrar o intervalo de valores que fazem com que a sentença seja verdadeira.
Para resolver uma inequação exponencial, utilizamos técnicas parecidas com as utilizadas para as equações exponenciais, ou seja, buscamos igualar as bases dos dois lados para conseguir comparar os seus expoentes. A diferença entre a equação exponencial e a inequação exponencial é que, na equação, existe uma igualdade e, na inequação, existe um símbolo de desigualdade.
Leia também: Inequação modular – expressão matemática que possui uma desigualdade e módulo
O que é inequação exponencial?

Exemplos:
-
2x > 32
-
0,5x ≤ 8
-
3x+1 + 4 ≤ 85
-
5x+1 < 252x–1
Para resolver uma inequação exponencial, utilizamos técnicas parecidas com as de resolução de equação, ou seja, buscamos igualar as bases. Contudo, as inequações exponenciais podem ser separadas em dois importantes casos, um deles é quando a base é maior que 1, e o outro é quando a base é um número entre 0 e 1. Observar a base é fundamental para conseguirmos encontrar o conjunto de soluções da inequação.
Propriedades da inequação exponencial
Para resolver as inequações exponenciais, é importante conhecer esses dois casos.
|
Quando a > 1 : ax > ay → x > y Quando 0 < a < 1 : ax > ay → x < y |
Então, ao igualar as bases, é fundamental observar se a base é maior que 1 ou se é um número entre 0 e 1.
Quando a base é um número maior que 1, ou seja, a > 1, mantemos a desigualdade entre os expoentes.
Exemplos:
a) 2x < 23
Sabemos que a base 2 é um número maior que 1, então, x < 3.
b) 5x ≥ 54
Sabemos que a base 5 é um número maior que 1, então, x ≥ 5.
Note que, nos dois casos, a desigualdade se manteve.
Quando a base é um número entre 0 e 1, ou seja, 0 > a > 1, invertemos a desigualdade.
Exemplos:
![]()
Nesse caso, a base é um número menor que 1 e maior que 0, então, invertemos a desigualdade entre os expoentes, logo, temos que: x < 6.
b) 0,3x ≤ 0,35
Sabemos que 0,3 é menor que 1 e maior que 0, então, inverteremos a desigualdade entre os expoentes, logo, temos que:
x ≥ 5
Veja também: Quais são as propriedades das desigualdades nas inequações?
Como resolver uma inequação exponencial?
Para resolver a inequação exponencial, buscamos igualar as bases dos dois lados da inequação, e, quando isso ocorre, observamos se base é maior que 1 ou se está entre 0 e 1, para escrever a inequação dos expoentes.
Exemplo 1:
2x < 8
Para encontrar as soluções possíveis para a equação, primeiro vamos igualar as bases. Para isso, fatoramos o 8.
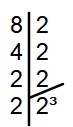
Reescrevendo a inequação exponencial trocando 8 por 2³:
2x < 2³
Como as bases são as mesmas e 2 é maior que 1, então, temos que:
x < 3
O conjunto de soluções dessa inequação é:
|
S= {x ∈ R | x < 3} |
Podemos fazer a representação geométrica dessa solução:
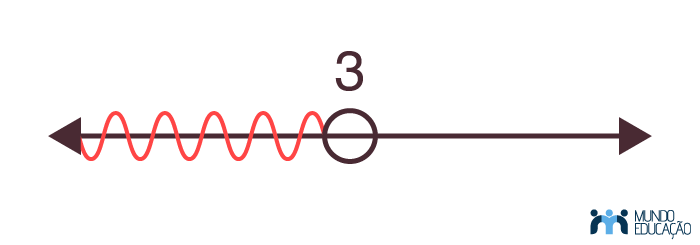
Exemplo 2:
![]()
Fatorando 81, temos que:
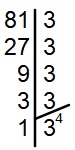
Para que a base seja a mesma, vamos escrever o inverso de 34 e trocar o sinal do expoente, então, temos que:
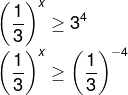
Como as bases foram igualadas, logo, podemos escrever a inequação do expoente. Contudo, note que a base é um número entre 0 e 1, quando isso acontece, é necessário inverter a desigualdade.
x ≤ -4
Então, o conjunto de soluções dessa inequação é:
|
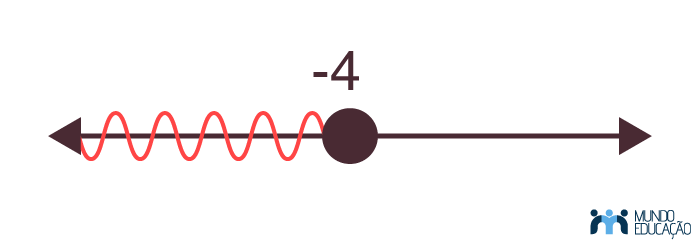
S = {x ∈ R | x ≤ -4} |
Fazendo a representação geométrica:
Exemplo 3:
5x+2 – 5x ≥ 3000
Para igualar as bases, vamos recorrer às propriedades de potência.
5x+2 – 5x ≥ 3000
5x · 52 – 5x ≥ 3000
Colocando 5x em evidência:
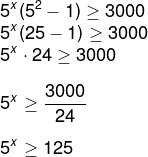
Fatorando 125:
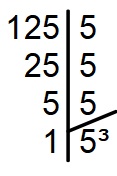
Sabemos que 125 = 5³, então, temos que:
5x ≥ 53
Como igualamos a base, podemos escrever a inequação com os expoentes. Note que a base é maior que 1, assim, temos que:
x ≥ 3
|
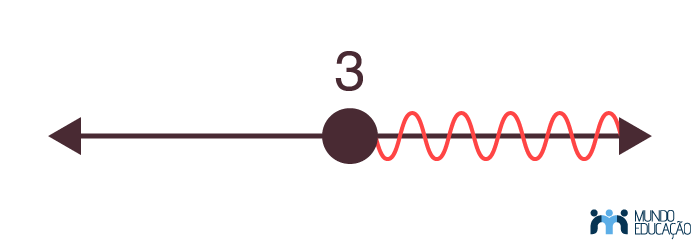
S = {x ∈ R | x ≥ 3} |
Representação geométrica:
Diferença entre inequação exponencial e equação exponencial
A diferença entre a inequação exponencial e a equação exponencial é que, na inequação exponencial, há um símbolo de desigualdade, e estamos encontrando um intervalo de números reais que fazem com que a sentença seja verdadeira. Já uma equação exponencial possui um sinal de igualdade, e, nesse caso, não encontramos um intervalo de soluções, mas sim alguns valores específicos que satisfazem a equação.
Exemplos:
3x < 3² → inequação exponencial
Note que a solução é x < 2, ou seja, qualquer valor que seja menor que 2 torna essa inequação verdadeira.
3x = 3² → equação exponencial
Note que a solução é x = 2, que é um único valor que satisfaz a equação.
Para saber mais informações e como resolver esse tipo de sentença matemática, leia o texto: Equação exponencial.
Exercícios resolvidos
Questão 1 - (UFRGS) A solução da inequação 0,5(1 – x) > 1é o conjunto:
A) S: {x ∈ R | x > 1}
B) S: {x ∈ R | x < 1}
C) S: {x ∈ R | x > 0}
D) S: {x ∈ R | x < 0}
E) Reais
Resolução
Alternativa A
Queremos resolver a inequação:
0,5(1 – x) > 1
Para igualar as bases, sabemos que todo número elevado a 0 é 1, então, 0,50 = 1, logo, temos que:
0,5(1 – x) > 0,50
Igualamos as bases. Como a base é menor que 1 e maior que 0, inverteremos a desigualdade:
1 – x < 0
-x < 0 – 1
-x < -1 · (-1)
Quando multiplicamos por -1, a desigualdade se inverte mais uma vez.
x > 1
S: {x ∈ R | x > 1}
Questão 2 - (ESPCEX) A inequação 10x + 10x+1 + 10x+2 + 10x+3 + 10x+4 < 11.111, em que x é um número real:
A) não tem solução.
B) tem apenas uma solução.
C) tem apenas soluções positivas.
D) tem apenas soluções negativas.
E) tem soluções positivas e negativas.
Resolução
Alternativa D
Utilizando a propriedade das potências, vamos separar, como uma multiplicação de potência de mesma base, as potências que possuem adição no expoente:
10x + 10x+1 + 10x+2 + 10x+3 + 10x+4 < 11.111
10x + 10x · 10¹ + 10x · 102 + 10x · 103 + 10x · 104 < 11.111
Colocando 10x em evidência:
10x · (1 + 101 + 102 + 103 + 104) < 11.111
10x · (1 + 10 + 100 + 1000 + 10.000) < 11.111
10x · 11.111 < 11.111
Agora, dividindo por 11.111:
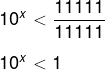
Para igualar as bases, sabemos que todo número elevado a 0 é 1, então, 100 = 1, logo, temos que:
10x < 100
x < 0
Como x é menor que 0, todas as soluções dessa equação são números negativos.
Artigos Relacionados

Últimas notícias
Outras matérias


















