Matriz Diagonal e Matriz identidade
Para que uma matriz tenha diagonal ela deverá ser uma matriz quadrada, então uma matriz diagonal é uma matriz quadrada onde os elementos que não pertencem à diagonal principal são obrigatoriamente iguais a zero.
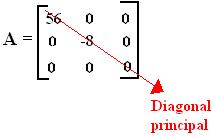
Portanto, podemos definir matriz diagonal como: Dado uma matriz C = (aij) n x n com
n ≥ 2é chamada de matriz diagonal se, somente se, i ≠ j for igual a zero.
Observação:
Isso não impede de os elementos que pertencem à diagonal principal sejam iguais a zero. Ou seja, uma matriz onde todos os seus elementos são iguais a zero é uma matriz diagonal.
A matriz identidade ou chamada também de matriz unidade é uma matriz quadrada de ordem n sendo que n ≥ 2, onde os elementos que pertencem à diagonal principal são sempre iguais a 1 e os outros elementos que não pertencem à diagonal principal são iguais a zero.
Essa matriz possui uma representação, sempre que for indicar uma matriz identidade pode-se escrever In.
Por exemplo:
Uma matriz identidade de ordem 2, será sempre escrita da seguinte forma:
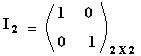
Uma matriz identidade de ordem 3, será sempre escrita da seguinte forma:
.jpg)
Uma matriz identidade de ordem 4, será sempre representada da seguinte forma:

Observando os exemplos acima de matriz identidade percebemos que para a construção de todas elas não foi preciso utilizar uma regra, é preciso apenas ter o conhecimento de qual é a sua ordem.
A matriz nula é uma matriz de qualquer ordem, sendo que todos os seus elementos são iguais a zero.
Observação:
A matriz identidade e a matriz nula são as únicas matrizes que não precisam de uma regra para sua construção, é preciso apenas saber qual é a sua ordem.
Portanto, podemos definir matriz diagonal como: Dado uma matriz C = (aij) n x n com
n ≥ 2é chamada de matriz diagonal se, somente se, i ≠ j for igual a zero.
Observação:
Isso não impede de os elementos que pertencem à diagonal principal sejam iguais a zero. Ou seja, uma matriz onde todos os seus elementos são iguais a zero é uma matriz diagonal.
A matriz identidade ou chamada também de matriz unidade é uma matriz quadrada de ordem n sendo que n ≥ 2, onde os elementos que pertencem à diagonal principal são sempre iguais a 1 e os outros elementos que não pertencem à diagonal principal são iguais a zero.
Essa matriz possui uma representação, sempre que for indicar uma matriz identidade pode-se escrever In.
Por exemplo:
Uma matriz identidade de ordem 2, será sempre escrita da seguinte forma:
Uma matriz identidade de ordem 3, será sempre escrita da seguinte forma:
.jpg)
Uma matriz identidade de ordem 4, será sempre representada da seguinte forma:
Observando os exemplos acima de matriz identidade percebemos que para a construção de todas elas não foi preciso utilizar uma regra, é preciso apenas ter o conhecimento de qual é a sua ordem.
A matriz nula é uma matriz de qualquer ordem, sendo que todos os seus elementos são iguais a zero.
Observação:
A matriz identidade e a matriz nula são as únicas matrizes que não precisam de uma regra para sua construção, é preciso apenas saber qual é a sua ordem.
Publicado por Danielle de Miranda
Assista às nossas videoaulas
Artigos Relacionados
Multiplicação de um número real por uma matriz
Matriz, Ordem das matrizes, Operação com matrizes, número real, multiplicação de número real por matriz, Adição e subtração de matrizes, Produto de matrizes, Produto.

Matemática do Zero
Matemática do Zero | Polígonos regulares e irregulares
Nessa aula veremos o que é um polígono, nomenclaruta de um polígono e como classificá-lo em regular e irregular.
Últimas notícias
Outras matérias
Biologia
Matemática
Geografia
Física
Vídeos

Saúde e bem-estar
Leptospirose
Foco de enchentes pode causar a doença. Assista à videoaula e entenda!

Gramática
Inglês
Que tal conhecer os três verbos mais usados na língua inglesa?

Matemática
Regra de três
Com essa aula você revisará tudo sobre a regra de três simples.















