Método da adição para sistemas com duas equações e duas incógnitas

Existem vários métodos que podem ser usados para resolver sistemas de equações. Um dos mais conhecidos é o método da adição. Ele visa a eliminar uma das incógnitas de um sistema pela soma dos termos semelhantes das equações que o compõem. No exemplo a seguir, observe que a simples soma dos termos das equações já zera uma das suas incógnitas:
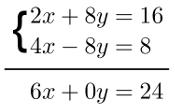
As somas realizadas nesse exemplo foram: 2x + 4x, 8y + (– 8y) = 0 e 16 + 8 = 24. Observe que, pelo resultado da soma, podemos encontrar o valor numérico de uma das incógnitas do sistema:
6x = 24
x = 24
6
x = 4
Para descobrir a incógnita y, basta substituir o valor numérico de x em uma das duas equações do sistema:
2x + 8y = 16
2·4 + 8y = 16
8 + 8y = 16
8y = 16 – 8
8y = 8
y = 8
8
y = 1
A solução desse sistema é S = {4, 1}.
Quando a soma dos termos não zera uma das incógnitas
O sistema do exemplo anterior foi resolvido com facilidade porque foi criado com os coeficientes da incógnita y opostas aditivas. Sempre que isso acontecer para uma das incógnitas, o método da adição é o mais indicado, pois os resultados são encontrados com muito mais agilidade.
Quando as incógnitas não forem opostas aditivas, ou seja, quando não forem o mesmo número com sinais diferentes, é necessário fazer um procedimento antes de somar as duas equações para que uma das incógnitas seja eliminada.
Para compreender esse procedimento, observe o exemplo a seguir:
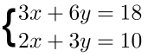
Observe que não é possível eliminar nenhuma das incógnitas, pois a soma das equações é:
5x + 9y = 28
Para viabilizar a eliminação de uma incógnita, devemos multiplicar uma das equações por uma constante para que pelo menos uma de suas incógnitas torne-se o inverso aditivo de uma das incógnitas da outra equação.
No exemplo, multiplicaremos a segunda equação por – 2. Esse valor foi escolhido para que o termo 3y tenha como resultado – 6y, que é o inverso aditivo de 6y da outra equação. Assim, é possível somar as duas, eliminando a incógnita y nesse processo.
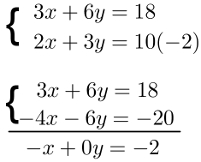
Observe que, ao multiplicar uma das equações por uma constante, todos os seus termos devem ser multiplicados por essa constante. Após a multiplicação, o sistema fica pronto para que a soma entre as equações seja feita. O resultado dessa soma é o seguinte:
– x = – 2
x = 2
Com o valor de uma das incógnitas, basta substituí-lo em uma das equações do sistema para descobrir o valor da outra incógnita:
3x + 6y = 18
3·2 + 6y = 18
6 + 6y = 18
6y = 18 – 6
6y = 12
y = 12
6
y = 2
A solução do sistema é S = {2, 2}
Artigos Relacionados

Últimas notícias
Outras matérias


















