Multiplicação de matrizes
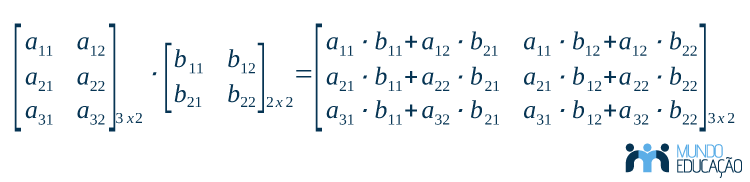
A multiplicação de matrizes é uma operação entre matrizes, conjuntos de dados divididos por linhas e colunas. Essa operação só pode ser realizada se o número de colunas da primeira matriz for igual ao número de linhas da segunda matriz. O resultado dessa multiplicação será uma nova matriz (a matriz produto) com a quantidade de linhas da primeira matriz e a quantidade de colunas da segunda matriz.
Leia também: Adição e subtração de matrizes — como fazer?
Resumo sobre multiplicação de matrizes
- A multiplicação de matrizes é uma operação que resulta em uma nova matriz, chamada de matriz produto.
- Os elementos da matriz produto são relações das linhas da primeira matriz com as colunas da segunda matriz.
- A multiplicação de matrizes só é possível quando o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz.
- Se a multiplicação existir, a matriz produto terá a quantidade de linhas da primeira matriz e a quantidade de colunas da segunda matriz.
- Para multiplicar um número real k por uma matriz A, basta multiplicar k por cada elemento de A.
- A matriz identidade é uma matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e os outros elementos são iguais a 0.
- A inversa de uma matriz M é uma matriz M-1 tal que M⋅M-1=I.
Videoaula sobre multiplicação de matrizes
Como calcular a multiplicação de matrizes?
A multiplicação de matrizes não é uma operação intuitiva. Enquanto a adição e subtração de matrizes são realizadas entre os elementos que ocupam a mesma posição, o processo de multiplicação é totalmente diferente.
Em primeiro lugar, não são quaisquer matrizes que podem ser multiplicadas. Assim, antes de fazer qualquer cálculo, é necessário analisar a condição de existência para essa operação.
Considere uma matriz A de ordem mxn e uma matriz B de ordem pxq. A multiplicação A⋅B, nessa ordem, só é possível se n = p. Isso significa que duas matrizes só podem ser multiplicadas se o número de colunas da primeira matriz for igual ao número de linhas da segunda matriz.
Além disso, supondo que a A⋅B exista, a matriz C resultante terá o número de linhas de A (primeira matriz) e o número de colunas de B (segunda matriz). No exemplo anterior, a ordem de C será mxq.
Mas como obter a matriz C, ou seja, como calcular a multiplicação A⋅B?
Considere cij o elemento da matriz C na linha i e coluna j. Cada elemento cij é a soma dos produtos entre os elementos correspondentes da linha i de A (primeira matriz) e da coluna j de B (segunda matriz). Parece difícil? Vejamos alguns exemplos para ilustrar esse processo.
- Exemplo 1:
Calcule a multiplicação A⋅B para as matrizes
\(A\ =\ \left[\begin{matrix}1&5\\3&2\\\end{matrix}\right] \ e \ B\ =\left[\begin{matrix}4&8\\7&0\\\end{matrix}\right]\)
Resolução:
Verificando a condição de existência para a multiplicação A⋅B: note que o número de colunas da matriz A é igual ao número de linhas da matriz B. Assim, existe a multiplicação A⋅B.
Considere C = A⋅B. Como o número de linhas de A é 2 e o número de colunas de B é 2, a ordem de C é 2x2.
\(C=\left[\begin{matrix}c_{11}&c_{12}\\c_{21}&c_{22}\\\end{matrix}\right]\)
Agora vamos encontrar cada elemento de C. Lembre-se de que cada elemento cij corresponde a uma relação entre a linha i de A e a coluna j de B:

Portanto,
\(\left[\begin{matrix}1&5\\3&2\\\end{matrix}\right]\cdot\left[\begin{matrix}4&8\\7&0\\\end{matrix}\right]\ =\ \left[\begin{matrix}c_{11}&c_{12}\\c_{21}&c_{22}\\\end{matrix}\right]\)
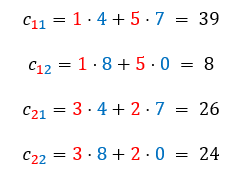
Logo,
\(C=\left[\begin{matrix}39&8\\26&24\\\end{matrix}\right]\)
- Exemplo 2:
Calcule a multiplicação B⋅A para as matrizes
\(A\ =\left[\begin{matrix}-2&7&9\\-1&5&8\\\end{matrix}\right] e\ B\ =\ \left[\begin{matrix}6&2\\0&-4\\3&1\\\end{matrix}\right]\)
Resolução:
Verificando a condição de existência para a multiplicação B⋅A: note que o número de colunas da matriz B é igual ao número de linhas da matriz A. Assim, existe a multiplicação B ⋅A.
Considere \(C\ =B\cdot A\). Como o número de linhas de B é 3 e o número de colunas de A é 3, a ordem de C é 3x3.
\(C=\left[\begin{matrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\\end{matrix}\right]\)
Agora vamos encontrar cada elemento de C. Observe que a multiplicação nesse caso é B⋅A:

Portanto,
\(\left[\begin{matrix}6&2\\0&-4\\3&1\\\end{matrix}\right]\cdot\left[\begin{matrix}-2&7&9\\-1&5&8\\\end{matrix}\right]\ =\ \left[\begin{matrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\\end{matrix}\right]\)
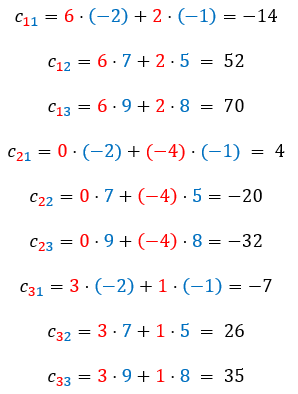
Logo,
\(C=\left[\begin{matrix}-14&52&70\\4&-20&-32\\-7&26&35\\\end{matrix}\right]\)
- Exemplo 3:
Calcule a multiplicação A⋅B para as matrizes
\(A\ =\ \left[\begin{matrix}9&3&0\\2&1&11\\-1&8&-6\\0&4&-12\\\end{matrix}\right] \ e\ B\ =\left[\begin{matrix}12&0&24&-1\\-5&16&1&3\\\end{matrix}\right]\)
Resolução:
Verificando a condição de existência para a multiplicação A⋅B: note que o número de colunas da matriz A (3) é diferente do número de linhas da matriz B (2). Assim, a multiplicação A⋅B não existe.
Importante: Vale destacar que, geralmente, a multiplicação de matrizes não é comutativa, ou seja, A ⋅B ≠B ⋅A. Considere o exemplo 3, em que a ordem de A é 4x3 e a ordem de B é 2x4. A multiplicação A⋅B não existe, mas a multiplicação B⋅A existe e resulta em uma matriz C de ordem 2x3.
Multiplicação de um número real por uma matriz
A multiplicação de um número real por uma matriz é outra operação envolvendo matrizes. Considere um número real k e uma matriz \(A=\left[a_{ij}\right]\). A multiplicação entre k e A resulta em uma matriz cujos elementos são o produto \(k\cdot a_{ij}\). Em outras palavras, para multiplicar um número real k por uma matriz A, basta multiplicar k por cada elemento da matriz A.
- Exemplo:
Considere \(k\ =\ 3 \ e\ A\ =\ \left[\begin{matrix}6&0&-2\\1&3&7\\\end{matrix}\right]\). Determine 2A.
Resolução:
\(2A\ =\ 2\cdot\left[\begin{matrix}6&0&-2\\1&3&7\\\end{matrix}\right]\)
\(2A\ =\ \left[\begin{matrix}2\cdot6&2\cdot0&2\cdot\left(-2\right)\\2\cdot1&2\cdot3&2\cdot7\\\end{matrix}\right]\)
\(2A\ =\ \left[\begin{matrix}12&0&-4\\2&6&14\\\end{matrix}\right]\)
Matriz identidade
A matriz identidade é a matriz quadrada (matriz que possui o número de linhas igual ao número de colunas) cujos elementos da diagonal principal são iguais a 1 e os demais elementos são iguais a 0. Essa matriz é representada pela notação In, em que n é a ordem da matriz.
- Exemplos:
\(I_2=\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\)
\(I_3=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
Uma propriedade importante da matriz identidade está relacionada à multiplicação de matrizes. Considere uma matriz quadrada A de ordem n. Assim, temos que
\(A\cdot I_n=I_n\cdot A=A\)
Matriz inversa
A matriz inversa da matriz M é a matriz M-1. Ela é assim chamada se
\(M\cdot M^{-1}=I\)
Isso significa que o produto entre uma matriz M e sua inversa resulta em uma matriz identidade.
Importante: Nem todas as matrizes apresentam inversa.
Veja também: Como determinar a igualdade entre matrizes?
Exercícios resolvidos sobre multiplicação de matrizes
Questão 1
(Unicamp) Considere a e b números reais tais que a matriz \(A\ =\left[\begin{matrix}1&2\\0&1\\\end{matrix}\right]\) satisfaz a equação \(A^2=aA+bI\), em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
A) – 2.
B) – 1.
C) 1.
D) 2.
Resolução:
Alternativa A.
Primeiro vamos calcular A2, ou seja, A⋅A. Como A é uma matriz quadrada, concluímos que essa multiplicação existe e resulta em uma matriz 2x2.
\(A^2=\left[\begin{matrix}1&2\\0&1\\\end{matrix}\right]\cdot\left[\begin{matrix}1&2\\0&1\\\end{matrix}\right]=\left[\begin{matrix}1\cdot1\ +\ 2\cdot0&1\cdot2\ +\ 2\cdot1\\0\cdot1\ +\ 1\cdot0&0\cdot2+1\cdot1\\\end{matrix}\right]\)
\(A^2=\left[\begin{matrix}1&4\\0&1\\\end{matrix}\right]\)
Ainda,
\(aA\ =\ a\ \cdot\left[\begin{matrix}1&2\\0&1\\\end{matrix}\right]\ =\ \left[\begin{matrix}a&2a\\0&a\\\end{matrix}\right]\)
\(bI\ =\ b\ \cdot\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]=\left[\begin{matrix}b&0\\0&b\\\end{matrix}\right]\)
Portanto,
\(A^2=aA+bI\)
\(\left[\begin{matrix}1&4\\0&1\\\end{matrix}\right]\ =\ \left[\begin{matrix}a&2a\\0&a\\\end{matrix}\right]\ +\left[\begin{matrix}b&0\\0&b\\\end{matrix}\right]\ \)
\(\left[\begin{matrix}1&4\\0&1\\\end{matrix}\right]\ =\ \left[\begin{matrix}a+b&2a\\0&a+b\\\end{matrix}\right]\)
Logo,
\( \begin{cases} a+b\ =\ 1\\ 2a\ =\ 4 \end{cases}\)
\(a\ =\ 2 \ e\ b\ =-1\)
Ou seja,
\(ab=-2\)
Questão 2
(FGV) Dada a matriz \(B=\left[\begin{matrix}3\\-4\\\end{matrix}\right]\) e sabendo que a matriz \(A^{-1}=\left[\begin{matrix}2&-1\\5&3\\\end{matrix}\right]\) é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a equação matricial AX = B, tem como soma de seus elementos o número
A) 14.
B) 13.
C) 15.
D) 12.
E) 16.
Resolução:
Alternativa B.
Multiplicando a equação AX = B por A-1 à esquerda, temos
\(A^{-1}\cdot A\cdot X=A^{-1}\cdot B\)
Como A-1 é inversa de A, então \(A^{-1}\cdot A\ =\ I\), em que I é a matriz identidade.
\(I\cdot X=A^{-1}\cdot B\)
Como I é a matriz identidade, \(I\ \cdot X\ =\ X\). Assim,
\(X\ =A^{-1}\cdot B\ \)
\(X\ =\left[\begin{matrix}2&-1\\5&3\\\end{matrix}\right]\cdot\left[\begin{matrix}3\\-4\\\end{matrix}\right]\ \)
\(X\ =\ \left[\begin{matrix}2\cdot3+\left(-1\right)\cdot\left(-4\right)\\5\cdot3+3\cdot\left(-4\right)\\\end{matrix}\right]\)
\(X\ =\ \left[\begin{matrix}10\\3\\\end{matrix}\right]\)
Portanto, a soma dos elementos é
10 + 3 = 13
Fontes
BOLDRINI, J. L. et al. Álgebra Linear. 3ª ed. São Paulo: Harper & Row do Brasil, 1980.
LIMA, Elon Lages. Álgebra Linear. Rio de Janeiro: IMPA, 2014
Artigos Relacionados

Últimas notícias
Outras matérias


















