Números primos

Números primos são aqueles divisíveis apenas por 1 e por eles mesmos. Estão presentes na Matemática desde a Antiguidade, e vários métodos foram desenvolvidos a fim de verificar se um número é de fato primo, como o Crivo de Erastóstenes.

O estudo dos números primos acabou resultando no Teorema Fundamental da Aritmética, que afirma que todo número inteiro positivo e maior que 1 pode ser representado de maneira única como um produto de fatores primos. Atualmente os números primos têm um papel fundamental no campo da criptografia e computação.

Leia também: Curiosidades sobre os números

Como saber se um número é primo ou não?

Uma das maneiras de descobrir se um número é primo é pela listagem dos seus divisores. Caso apareça mais números além do 1 e do número a ser verificado, o número não é primo e é chamado de número composto.

• Exemplos

1. Verifique quais dos números entre 2, 3, 10, 20, 35 e 100 são primos.

Para isso, vamos escrever os divisores de cada um desses números.

D(2) = {1;2}

D(3) = {1;3}

D(10) = {1;2;5;10}

D(20) = {1;2;4;5;10;20}

D(35) = {1;5;7;35}

D(100) = {1;2;4;5;10;20;25;50;100}

Perceba que, de todos os números listados, somente os números 2 e 3 possuem como divisores o 1 e si próprio. Logo, da listagem acima, somente os números 2 e 3 são primos e 10, 20, 35 e 100 são compostos.

Mas você percebeu que, à medida que o valor dos números cresce, mais complicado fica de listar os seus divisores? Nos dias atuais, é um grande desafio para matemáticos e computadores determinar se um número é ou não primo.

Existe uma ferramenta que possibilita verificarmos se números maiores são primos ou não, mas mesmo essa ferramenta possui limitações para números relativamente maiores. Essa ferramenta foi desenvolvida por Erastóstenes, matemático grego, e foi denominada como Crivo de Erastóstenes.

Veja também: 3 erros comuns ao resolver expressões numéricas

• Crivo de Erastóstenes

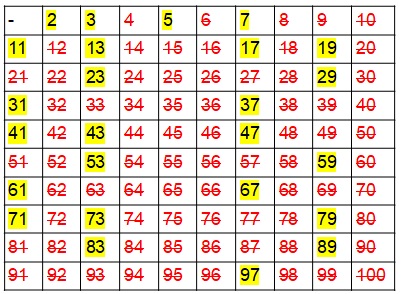
O Crivo de Erastóstenes consiste em criar uma tabela com números que vão de 2 até o número desejado, visto que o número 1 não é primo. Em seguida, realizamos os seguintes passos:

Passo 1 – Tendo em vista as regras de divisibilidade, sabemos que o único número par primo é o número dois. Então, excluímos todos os demais pares da tabela, ou seja, os múltiplos de 2.

4,6,8,10,12,...

Passo 2 - De acordo com as regras de divisibilidade por 3, sabemos que um número é divisível por 3 caso a soma dos algarismos também seja. Assim, vamos excluir todos os números que são múltiplos de 3.

6,9,12,15,18,..., 321,324,...

Passo 3 – Do critério de divisibilidade por 5, sabemos que um número é divisível por 5 caso ele termine em 0 ou em 5. Vamos excluir todos os números que terminam em 0 e em 5.

10,15,20,15,30,...,5920,5925,...

Passo 4 – De maneira análoga, verificando o critério de divisibilidade, vamos excluir todos os múltiplos de 7.

14,21,28,35,...,539,546,...

Feito todo esse processo, os números que sobrarem são os primos de 2 até o número desejado.

• Exemplo

Determine os números primos menores que 100.

Inicialmente vamos construir uma tabela de 2 até 100:

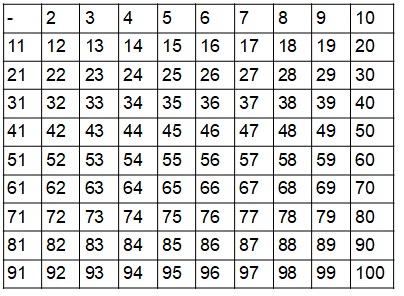
Aplicando todos os passos, vamos ter a seguinte tabela:

Teorema Fundamental da Aritmética

O Teorema Fundamental da Aritmética é muito importante quando se fala de decomposição em fatores primos. O teorema afirma que:

Todo número inteiro maior que 1 pode ser representado como uma multiplicação de fatores primos.

Leia também: Múltiplos e divisores: o que são e como encontrar

Decomposição em fatores primos

Como dito, o Teorema Fundamental da Aritmética garante que todo número composto, com exceção do 1, pode ser escrito como forma de multiplicação de números primos.

Para encontrar a forma fatorada de determinado número primo, basta realizar divisões sucessivas por números primos.

• Exemplos

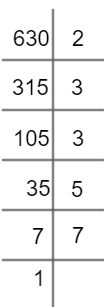
Vamos determinar a forma fatorada do número composto 630.

Passo 1 – Dividir o número dado pelo primeiro possível, nesse caso o número 2, por se tratar de um número par. Assim:

630 = 315 ∙ 2

Passo 2 – Pegamos o resultado da divisão e realizamos o mesmo processo. Note que 315 não é divisível por 2, então buscamos outro número primo. Pode ser o número 3, já que a soma de seus algarismos é divisível por 3. Assim:

630 = 105 ∙ 3

Passo 3 – O mesmo processo deve ser aplicado ao 105, ou seja, vamos dividi-lo por 3 novamente. Logo,

105 = 35 ∙ 3

Passo 4 – Dividindo o número 35 por 5, temos:

35 = 7 ∙ 5

Passo 5 - Dividindo o 7 por ele mesmo, pois, por ser primo, só pode ser divisível por 1 e ele mesmo, temos:

7 = 1 ∙ 7

Quando o quociente, que é o resultado da divisão, for igual a 1, o processo de decomposição chega ao fim. Assim, o número 630 na forma fatorada é:

630 = 2 ∙ 3 ∙ 3 ∙ 5 ∙ 7

630 = 2 ∙ 3² ∙ 5 ∙ 7

Existe uma notação que simplifica todo o processo de decomposição. Veja a seguir: