O que é plano?

Planos são figuras geométricas bidimensionais formadas pela reunião de infinitas retas, perpendiculares a uma reta dada, dispostas lado a lado. Essa figura é considerada na Geometria como um conceito primitivo. Isso acontece porque, na realidade, não existe definição para ponto, reta e plano. Temos apenas uma “ideia primitiva” de como essas figuras são e/ou do seu formato.
Os planos podem ser formados por retas, assim como as retas podem ser formadas por pontos. Uma reta é um conjunto de pontos que não faz curva. Um plano, por sua vez, é um conjunto de retas que não faz curva.
Os planos geralmente são definidos em um espaço tridimensional. É sobre eles que são construídas todas as formas geométricas planas e as propriedades que as envolvem. Além disso, como veremos a seguir, duas retas concorrentes são suficientes para definir um plano. Quando essas duas retas estão graduadas, o plano resultante é chamado de “Plano Cartesiano” e é usado para localização e para definir toda a Geometria Analítica plana.
Também existem as planificações. Nelas o contorno de um sólido geométrico tridimensional é “desdobrado” e colado sobre um plano, gerando uma figura conhecida como “planificação”.
Postulados
Os postulados, também conhecidos como axiomas, são fatos tomados como verdadeiros para dar origem a teoremas e propriedades que devem ser provados. O primeiro postulado envolvendo planos é o da existência:
“Existe plano e tanto nele quanto fora dele existem infinitos pontos.”
Esse postulado foi criado para assumir que planos existem, uma vez que não é possível provar sua existência. Além disso, também é preciso afirmar que existem pontos tanto dentro quanto fora do plano para relacioná-los.
O segundo postulado sobre planos é o da inclusão:
“Se um plano contém dois pontos distintos de uma reta, ele contém toda essa reta.”
Também não é possível demonstrar que as retas são realmente retas, pois elas são definidas apenas como conjuntos de pontos. Esse postulado afirma que um plano contém todos os pontos de uma reta se ele possui pelo menos dois pontos distintos dela.
Outros dois postulados indicam os resultados de traçar uma reta em um plano ou de traçar um plano no espaço. Esses dois postulados estão unidos em um só a seguir:
“Uma reta divide um plano em duas partes nas quais ela está contida. Um plano divide o espaço em duas partes nas quais ele está contido.”
Determinando planos
O último axioma, o postulado da determinação, possibilita a criação de um plano a partir de um número finito de pontos:
“Três pontos não colineares determinam um plano.”
Sendo assim, é possível construir planos de quatro maneiras distintas:
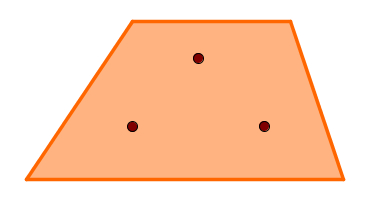
1 – Três pontos não colineares determinam um plano.
Isso acontece em virtude do axioma que acabamos de descrever.
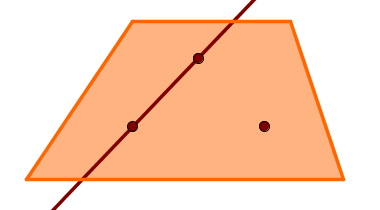
2 – Um ponto e uma reta fora dele determinam um plano.
Se existe um ponto fora de uma reta, basta escolher dois pontos distintos pertencentes a ela para obter três pontos não colineares, que determinam um plano.
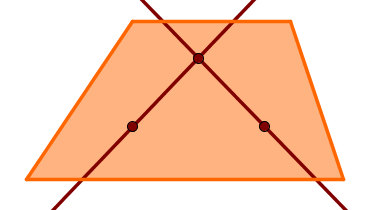
3 – Duas retas concorrentes determinam um plano.
Retas concorrentes são aquelas que possuem apenas um ponto de intersecção. Para encontrar três pontos não colineares, faça o seguinte: escolha o ponto de intersecção entre essas retas, um ponto qualquer na primeira e um ponto qualquer na segunda, exceto, é claro, o próprio ponto de intersecção. Com esses três, caímos no caso do postulado de determinação.
4 – Duas retas paralelas determinam um plano.
Para encontrar três pontos e cair no caso do axioma de determinação, basta tomar apenas um ponto na primeira reta e dois pontos distintos na segunda.
.jpg)
Por Luiz Paulo Moreira
Graduado em Matemática
Artigos Relacionados

Últimas notícias
Outras matérias


















