Operações com os números racionais

Pertencem ao conjunto dos racionais os números positivos, negativos, decimais, frações e dízimas periódicas. Representamos esse conjunto por meio da letra Q maiúscula:
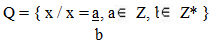
Lê-se: O conjunto dos números racionais é igual a x, tal que x é igual a (a) sobre (b), (a) pertence ao conjunto dos inteiros e (b) pertence ao conjunto dos inteiros com a ausência do zero.
É possível realizar as quatro operações com os números racionais. Entre essas operações, podemos destacar:
-
Soma de duas ou mais frações:
Para somar duas ou mais frações, é necessário que o denominador em todas as frações seja o mesmo. Após verificar isso ou reduzir os denominadores a um mesmo valor por meio do Mínimo Múltiplo Comum (MMC) ou das frações equivalentes, basta conservar o denominador e somar os expoentes. Veja:
Utilizando o MMC para reduzir os denominadores:
1 + 2 + 4 = 1 + 2 + 4 = 3 + 4 + 24 = 31
2 3 2 3 1 6 6
Cálculo do MMC
2, 3, 1| 2
1, 3, 1| 3
1, 1, 1|
MMC (2, 3, 1) = 2 x 3 = 6
Para obter os números do numerador, foi feito o seguinte:
6 : 2 = 3 x 1 = 3
6 : 3 = 2 x 2 = 4
6 : 1 = 6 x 4 = 24
Utilizando as frações equivalentes:
1 x 3+ 2 x 2+ 4 x 6= 3 + 4 + 24 = 31
2 x 3 3 x 2 1 x6 6 6 6 6
-
Soma de dois ou mais números decimais
Na soma de números decimais, juntamos número inteiro com inteiro, parte decimal com decimal, parte centesimal com centesimal e assim por diante. Observe o exemplo abaixo:
2,57 + 1,63 =
2 e 1: partes inteiras
0,5 e 0,6: partes decimais
0,07 e 0,03: partes centesimais
Para resolver a soma de números decimais, podemos estruturar o algoritmo da adição.
2,57
+ 1,63
4,20
Podemos também somar números decimais por meio de frações. Para isso, basta transformar cada número decimal em uma fração. Confira o exemplo abaixo:
2,57 + 1,63 = → Represente os números decimais na forma de fração;
= 257 + 163 = → Como o denominador em ambas as frações é 100, podemos somá-los.
100 100
= 420 = → Realize a divisão de 420 por 100.
100
= 4,20
-
Subtração de duas ou mais frações:
O processo de subtração de fração é semelhante ao da soma. A diferença está no sinal da operação, que será de menos. Observe:
5 – 3 – 2 = 5 +( – 3 ) + ( – 2 )= 20 – 9 – 24 = – 13
3 4 3 ( 4 ) 12 12
Cálculo do MMC:
3, 4, 1| 2
3, 2, 1|2
3, 1, 1|3
1, 1, 1|
Para obter os números do numerador, fizemos o seguinte:
12 : 3 = 4 x 5 = 20
12 : 4 = 3 x – 3 = – 9
12 : 1 = 12 x – 2 = – 24
-
Subtração de dois ou mais números decimais:
Devemos subtrair número inteiro com inteiro, parte decimal com decimal, parte centesimal com centesimal e assim por diante. Confira o exemplo abaixo:
3,15 – 2,04 – 1 =
Para resolver essa subtração de números decimais, devemos subtrair os dois primeiros termos da esquerda para a direita (3,15 – 2,04).
3,15
- 2,04
1,11
Agora temos que subtrair 1,11 – 1 =
1,11
- 1,00
0,11
Podemos também resolver o exemplo anterior por meio da subtração de frações. Acompanhe:
3,15 – 2,04 – 1 = → Transforme os números 3,15 e 2,04 em frações.
= 315 – 204 – 1 = → Como os denominadores das frações são iguais, faça a subtração dos numeradores.
100 100
= 111 – 1 = → Como os denominadores das frações são diferentes, devemos reduzi-los ao mesmo
100 1 denominador. O MMC (100, 1) é 100.
= 111 – 100 = → Como reduzimos para o mesmo denominador, podemos subtrair os numeradores.
100
= 11 = → Faça a divisão de 11/100
100
= 0,11
-
Multiplicação de frações
Na multiplicação de frações, devemos multiplicar os numeradores com numeradores e os denominadores com denominadores. Confira:
3 x 6 = ( 3 x 6 ) = 18 → Como a fração não está na forma irredutível, temos que simplificá-la.
7 4 ( 7 x 4 ) 28
3 x 6 = ( 3 x 6 ) = 18 : 2 = 9
7 4 ( 7 x 4 ) 28 : 2 14
-
Multiplicação de números decimais
Ao multiplicarmos números decimais, devemos estruturar o algoritmo. Para saber a posição da vírgula no produto obtido, contamos quantas casas decimais possui cada número decimal e deslocamos a vírgula em relação aos algarismos do produto da direita para a esquerda. Observe o exemplo:
2,4 x 1,2 = → Inicialmente estruture o algoritmo da multiplicação.
2,4
x 1,2
+ 48
24
2,88 → Observe que a vírgula ficou entre os algarismos 2 e 6. Isso aconteceu porque o número 2,4 possui uma casa decimal, e o número 1,2 também possui uma casa decimal. Assim, temos, no total, duas casas decimais. Sendo assim, devemos deslocar a vírgula do produto obtido (288) duas casas da direita para a esquerda (2,88).
Poderíamos também resolver esse exemplo por meio de frações.
2,4 x 1,2 = → Transforme os números decimais em frações.
= 24 x 12 = → Multiplique os numeradores (24 x 12) e os denominadores (10 x 10).
10 10
= 288 = → Faça a divisão de 288 por 100.
100
= 2,88
-
Divisão de duas ou mais frações
Para dividirmos duas ou mais frações, utilizamos uma regra prática: conserva-se a primeira fração, multiplicando-a pelo inverso da segunda. Recorde-se que o inverso de uma fração é dado ao trocarmos o seu denominador pelo numerador. Veja:
13 : 9 = 13 x 2 = 26
7 2 7 9 63
1 : 4 : 2 = (1 : 4 ) : 2 = ( 1 x 5 ) : 2 = 5 : 2 = 5 x 6 = 30 :2 = 15
2 5 6 ( 2 5 ) 6 ( 2 x 4 ) 6 8 6 8 x 2 16 : 2 8
-
Divisão de dois ou mais números decimais
Para realizar a divisão de números decimais, devemos igualar a quantidade de casas decimais dos números e efetuar a divisão. Confira o exemplo abaixo:
1,23 : 0,5 = → O número 1,23 possui duas casas decimais, e o número 0,5 possui uma casa decimal. Para igualar a quantidade de casas decimais, devemos multiplicar ambos os números pelo termo decimal, ou seja, 10, 100, 1000..., que possui a maior quantidade de casas decimais. Sendo assim, temos que multiplicar 1,23 e 0,5 por 100.
(1,23 x 100) : (0,5 x 100) = 123 : 50 → Utilizando o algoritmo da divisão, temos 123 : 50.
123 |50
- 100 2,46
230
- 200
300
- 300
0
1,23 : 0,5 = 2,46
Veja agora como transformar os números decimais do exemplo anterior em frações:
1,23 : 0,5 = → Transforme os números decimais em frações.
= 123 : 5 = → Aplicando a regra aprendida anteriormente, conserve a primeira fração e
100 10 multiplique-a pelo inverso da segunda.
= 123 x 10 = → Faça o produto dos numeradores e dos denominadores.
100 5
= 1230 = → Realize a divisão de 1230 por 500.
500
= 2,46
-
Soma, subtração, multiplicação e divisão de dízimas periódicas
A dízima periódica é um número decimal em que os algarismos após a vírgula repetem-se infinitamente. Exemplos: 1,222..., 1,2323..., 2,23562356...
A repetição desses algarismos após a vírgula é chamada de período. Veja:
-
O período de 1,222... é 2.
-
O período de 1,2323... é 23.
-
O período de 2,23562356... é 2356.
Para realizar a soma, subtração, multiplicação e divisão de dízimas periódicas, devemos descobrir o período e aplicar as definições aprendidas anteriormente para números decimais, haja vista que a dízima periódica é um número decimal. Vejamos alguns exemplos:
-
Soma de dízima periódica
2,333... + 1,555... =
O período de 2,333... é 3, e o período de 1,555... é 5. Realizando a soma, temos:
2,3
+1,5
3,8
-
Subtração de dízima periódica
3,6565... - 1,222... =
O período de 3,6565... é 65, e o período de 1,222... é 2. Fazendo o algoritmo da subtração, temos:
3,65
- 1,22
2,43
-
Multiplicação de dízima periódica
5,2323... x 1,111... =
O período de 5,2323... é 23, e o período de 1,111... é 1. Efetuando o produto, temos:
5,23
x 1,11
523
+ 523
523
5,8053
A multiplicação resultou em: 5,2323... x 1,111... = 5,23 x 1,11 = 5,8053
-
Divisão de dízima periódica
2,5252 … : 0,555... =
O período de 2,5252... é 52, e o período de 0,555... é 5. Realizando a divisão, temos:
2,52 : 0,5 = (2,52 x 100) : ( 0,5 x 100) = 252 : 50
252 | 50
- 250 5,04
200
- 200
0
A divisão de: 2,5252 … : 0,555... = 2,52 : 0,5 = 5,04
Artigos de Operações com os números racionais

Últimas notícias
Outras matérias


















