Poliedros regulares
Poliedros são sólidos geométricos limitados por polígonos, que, por sua vez, são figuras geométricas planas limitadas por segmentos de reta. Um poliedro é dito regular quando obedece às três exigências seguintes:
1) é convexo;
2) é também poliedro de Platão;
3) Os polígonos que o formam, chamados de faces, são regulares e congruentes.
Todo poliedro regular é um poliedro de Platão, mas existem poliedros de Platão que não são regulares. Veja a seguir uma explicação sobre cada uma das condições para que um poliedro seja regular.
→ O que é um poliedro convexo?
Para compreender a ideia de poliedro convexo, é preciso saber a seguinte definição dos planos no espaço: Todo plano divide o espaço em dois semiespaços. Essa propriedade é parecida com a de semirreta. É comparável ainda com uma secção no espaço que o divide ao meio. Qualquer face de um poliedro está contida em um plano – por ser uma figura plana – e, por isso, determina um corte no espaço, dividindo-o.
Um poliedro é convexo quando está inteiramente contido em um dos dois semiespaços determinados por qualquer uma de suas faces.
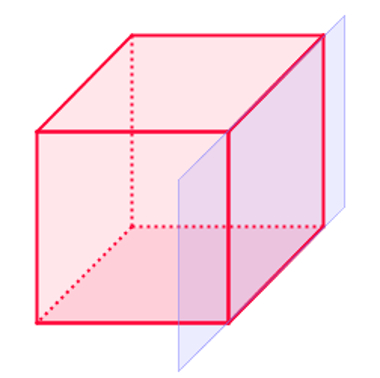
A figura acima é um poliedro convexo. Para ilustrar isso, colocamos um plano na cor lilás em uma de suas faces, mas a mesma ideia aplica-se para qualquer face.
Dessa maneira, quando há pelo menos uma face de um poliedro que determina dois semiespaços, nos quais existem partes do poliedro, esse poliedro não é convexo.
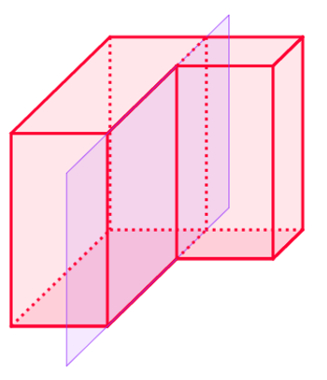
A figura acima não é convexa, pois existe uma face, contida no plano representado pelo quadrilátero roxo, que determina dois semiespaços. Como existem partes do poliedro em ambos, ele não é convexo.
→ O que é um poliedro de Platão?
Os poliedros de Platão são aqueles que possuem as seguintes propriedades:
1) Todas as faces apresentam o mesmo número de arestas;
2) Todos os vértices possuem o mesmo número de arestas, isto é, se um vértice é a extremidade de três arestas, por exemplo, então todos serão também.
3) É convexo;
4) Seja o número de faces igual a F, de arestas igual a A e de vértices igual a V, então vale a seguinte relação, chamada de relação de Euler:
V – A + F = 2
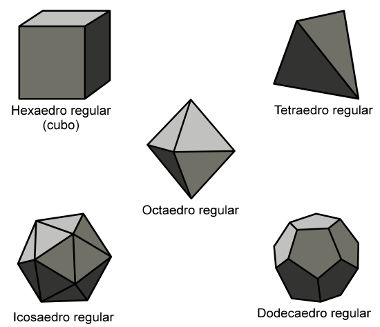
Existem infinitos poliedros de Platão, contudo, todos eles são um dos cinco seguintes, variando apenas em dimensões:
1) Tetraedro regular;
2) Hexaedro regular, mais conhecido como cubo;
3) Octaedro regular;
4) Dodecaedro regular;
5) Icosaedro regular.
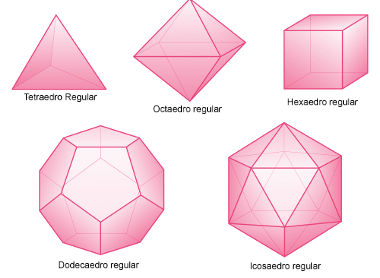
Imagens dos poliedros mencionados acima
→ O que é um polígono regular?
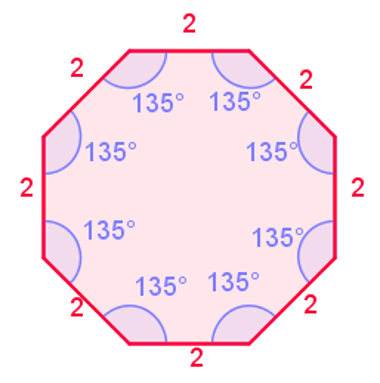
São polígonos convexos que possuem todos os lados e ângulos congruentes. A imagem abaixo ilustra um polígono convexo.
Artigos Relacionados

Últimas notícias
Outras matérias


















