Princípios da geometria
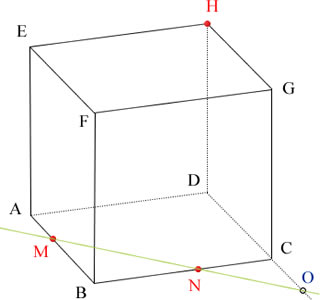
Quando iniciamos o estudo de geometria é necessário que saibamos alguns princípios importantes e essenciais para o aprendizado de Geometria Plana ou Geometria de espacial.
►Ponto
Na matemática ponto não tem uma definição, mas é representado por letras maiúsculas: A, B, C,D, ... , Z), Veja alguns exemplos:
.jpg)
A, B e P representam pontos.
►Reta
Para formarmos uma reta precisamos de no mínimo dois pontos. A reta é representada por letras minúsculas (a, b, .... , r, s, t, .....,z), e em suas extremidades temos setas, pois a reta é infinita para os dois sentidos.
.jpg)
• Para fazermos a relação de ponto e reta usamos a relação de pertinência:
A t (A pertence a t)
t (A pertence a t)
Encontramos retas em algumas coisas do nosso cotidiano: como o encontro de duas paredes, lado de uma mesa, cabo de vassoura, são aproximações grosseiras de retas, mas que nos ajuda a visualizar melhor.

Além de usarmos as letras minúsculas na representação das retas, podemos utilizar os seus pontos na sua representação:
.jpg)
Temos no exemplo acima uma reta a letra que a representa é t. Pertencem a reta t os pontos A e G, então podemos fazer uma outra representação para a reta t:
.jpg) -------- sempre em cima dos pontos deve ser colocado uma reta com duas setas
-------- sempre em cima dos pontos deve ser colocado uma reta com duas setas
pois a reta pode ser prolongada nos dois sentidos.
►Plano
Para diferenciarmos a representação do plano com a representação da reta, a sua representação ficou com letras minúsculas, mas do alfabeto grego: α (alfa), β (beta), ...
Como a reta o plano também é infinito.
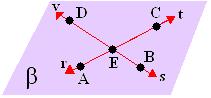
Em um plano β estão contidas retas e tem pontos que pertencem a esse mesmo plano:
• Para fazermos uma relação entre ponto e reta utilizamos a relação de pertinência:
A r ; B
r ; B  s ; C
s ; C t ; D
t ; D  v ; E
v ; E r
r
• Para fazermos uma relação entre ponto e plano utilizaremos a relação de pertinência:
A β ; B
β ; B  β ; C
β ; C  β ; D
β ; D β ; E
β ; E  β
β
• Para fazer a relação entre reta e plano, utilizamos a relação de inclusão:
v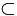 β ; r
β ; r 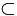 β ; t
β ; t 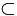 β ; s
β ; s 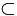 β
β
►Ponto
Na matemática ponto não tem uma definição, mas é representado por letras maiúsculas: A, B, C,D, ... , Z), Veja alguns exemplos:
.jpg)
A, B e P representam pontos.
►Reta
Para formarmos uma reta precisamos de no mínimo dois pontos. A reta é representada por letras minúsculas (a, b, .... , r, s, t, .....,z), e em suas extremidades temos setas, pois a reta é infinita para os dois sentidos.
• Para fazermos a relação de ponto e reta usamos a relação de pertinência:
A
Encontramos retas em algumas coisas do nosso cotidiano: como o encontro de duas paredes, lado de uma mesa, cabo de vassoura, são aproximações grosseiras de retas, mas que nos ajuda a visualizar melhor.
Além de usarmos as letras minúsculas na representação das retas, podemos utilizar os seus pontos na sua representação:
Temos no exemplo acima uma reta a letra que a representa é t. Pertencem a reta t os pontos A e G, então podemos fazer uma outra representação para a reta t:
pois a reta pode ser prolongada nos dois sentidos.
►Plano
Para diferenciarmos a representação do plano com a representação da reta, a sua representação ficou com letras minúsculas, mas do alfabeto grego: α (alfa), β (beta), ...
Como a reta o plano também é infinito.
Em um plano β estão contidas retas e tem pontos que pertencem a esse mesmo plano:
• Para fazermos uma relação entre ponto e reta utilizamos a relação de pertinência:
A
• Para fazermos uma relação entre ponto e plano utilizaremos a relação de pertinência:
A
• Para fazer a relação entre reta e plano, utilizamos a relação de inclusão:
v
Publicado por Danielle de Miranda
Artigos Relacionados
Aplicações do Teorema de Tales
Clique aqui e aprenda quando e como utilizar o Teorema de Tales!
Fórmulas para Cálculo de Volume de sólidos
Aprenda fórmulas para calcular o volume de sólidos, tendo em vista sua forma e dimensões.

Português
A representação indígena na literatura brasileira
A figura do indígena sempre esteve presente na literatura brasileira. Mas de que forma essa cultura foi representada? Quais são as implicações dessas imagens na construção do imaginário e da identidade cultural do povo brasileiro?
Últimas notícias
Outras matérias
Biologia
Matemática
Geografia
Física
Vídeos

Saúde e bem-estar
Leptospirose
Foco de enchentes pode causar a doença. Assista à videoaula e entenda!

Gramática
Inglês
Que tal conhecer os três verbos mais usados na língua inglesa?

Matemática
Regra de três
Com essa aula você revisará tudo sobre a regra de três simples.















