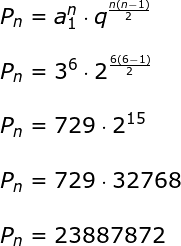Produto dos termos de uma PG finita

Uma progressão geométrica (PG) é uma sequência de números em que cada termo é igual ao produto de seu antecessor com uma constante q, chamada de razão da PG. Uma das operações que envolvem esse tipo de sequência é o cálculo da soma dos termos de uma PG finita e de uma PG infinita. Também podemos calcular o produto dos termos de uma PG quando ela é finita. A fórmula usada para isso é:
Nessa fórmula, Pn é o resultado, ou seja, o produto dos termos da PG, a1 é o primeiro termo, “q” é a razão da PG e “n” é seu número de termos.
Demonstração
Para mostrar que o produto dos termos de uma PG pode ser obtido pela fórmula dada, devemos rever alguns conceitos em exemplos para utilizá-los na multiplicação de uma PG de “n” termos.
Dada a PG (2, 4, 8, 16, 32, …). Perceba que cada termo dela é igual ao produto do seu antecessor com a constante 2. Assim, podemos escrever todos os termos dessa PG em função do primeiro:
a1 = 2
a2 = 4 = a1·2
a3 = 8 = a1·2·2
a4 = 16 = a1·2·2·2
a5 = 32 = a1·2·2·2·2
…
Essas igualdades podem ser escritas da seguinte maneira:
a1 = 2
a2 = a1·2
a3 = a1·22
a4 = a1·23
a5 = a1·24
…
Observe que o expoente relacionado à razão 2 sempre é uma unidade menor do que o índice do termo analisado.
Dito isso, veja como é a sequência de termos de uma PG qualquer finita, com n termos e razão q:
a1 = a1
a2 = a1·q
a3 = a1·q2
a4 = a1·q3
a5 = a1·q4
…
an = a1·qn – 1
Sabemos que os expoentes relacionados à razão são sempre uma unidade menor do que o índice do termo analisado, por isso o expoente do último termo da PG deverá ser n – 1. Agora, confira o produto dos termos dessa PG:
Pn = a1·a2·a3·…·an
Escrevendo todos esses termos em função do primeiro termo (a1), temos:
Pn = a1·a1·q· a1·q2·…·a1·qn – 1
Observe que o termo a1 aparece n vezes nessa multiplicação. Perceba também que q aparece n – 1 vezes (pois o primeiro termo não é multiplicado pela razão). Separando os termos e a propriedade da soma de potências de bases iguais, temos:
(1) Pn = a1n·q1 + 2 + … + n – 1
Note que a soma dos expoentes de q formam a soma de uma PA de razão 1. A soma dos termos de uma PA finita é dada pela seguinte fórmula:
Sn = (b1 + bn)·n
2
Sn = [1 + (n – 1)]·(n – 1)
2
Sn = n·(n – 1)
2
Substituindo essa soma na expressão 1, temos:
Exemplo
Encontre o produto dos termos da PG a seguir, sabendo que ela possui seis termos.
(3, 6, 12, …)
Solução:
A razão dessa PG é 2, e o primeiro termo é 3. Sabendo que essa progressão possui seis termos, substitua esses valores na fórmula:
Artigos Relacionados

Últimas notícias
Outras matérias