Triângulo equilátero
Conhecemos como triângulo equilátero o triângulo que possui três lados congruentes, ou seja, todos os seus lados possuem as mesmas medidas, e, por isso, ele tem propriedades específicas e importantes de serem aprendidas. Em um triângulo equilátero, além dos lados, todos os ângulos internos são congruentes, medindo 60° cada.
A altura de um triângulo equilátero é também bissetriz e mediana. Para calcular a área, a altura e o perímetro dessa figura, existem fórmulas específicas. Além do triângulo equilátero, existem outros dois tipos de triângulo quando analisamos seus lados, que são o isósceles e o escaleno.
Leia mais: Geometria plana — é a área da matemática que estuda as figuras planas
Resumo sobre triângulo equilátero
-
Um triângulo equilátero possui todos os lados congruentes.
-
Os ângulos internos do triângulo equilátero medem 60° cada.
-
Para calcular a altura de um triângulo, utilizamos a fórmula:
![]()
-
Para calcular a área de um triângulo equilátero, utilizamos a fórmula:
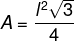
-
Existem outros tipos de triângulos quando os classificamos quanto aos seus lados, são eles:
-
triângulo isósceles: dois lados congruentes;
-
triângulo escaleno: todos os lados com medidas diferentes.
-
Características do triângulo equilátero
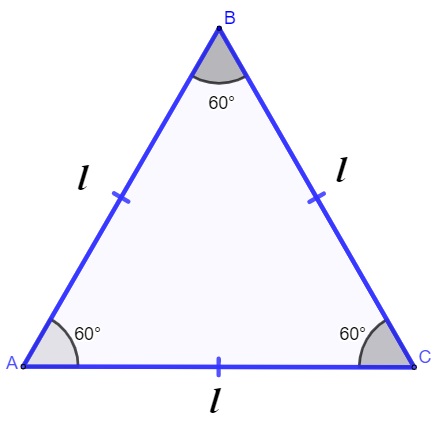
Um triângulo é equilátero quando possui todos os lados congruentes, ou seja, todos os lados têm as mesmas medidas, e cada lado mede 60º.
Propriedades do triângulo equilátero
O triângulo equilátero possui propriedades específicas devido aos seus lados serem congruentes, além das propriedades já existentes para todos os triângulos.
1ª propriedade: os ângulos internos de um triângulo equilátero possuem sempre 60º.
Sabemos que a soma dos ângulos internos de um triângulo qualquer é 180º, como em um triângulo equilátero todos os ângulos são congruentes, então 180 : 3 = 60°.
2ª propriedade: a altura relativa a um dos seus lados é também a bissetriz e a mediana.
Vale lembrar que:
-
A altura é o segmento de reta perpendicular à base do triângulo.
-
A mediana é o segmento de reta que liga o vértice ao ponto médio do lado oposto a ele.
-
A bissetriz é o segmento de reta que divide o ângulo em dois ângulos congruentes.
Caso queira saber mais sobre o tema deste tópico, leia: Propriedades do triângulo equilátero.
Altura do triângulo equilátero
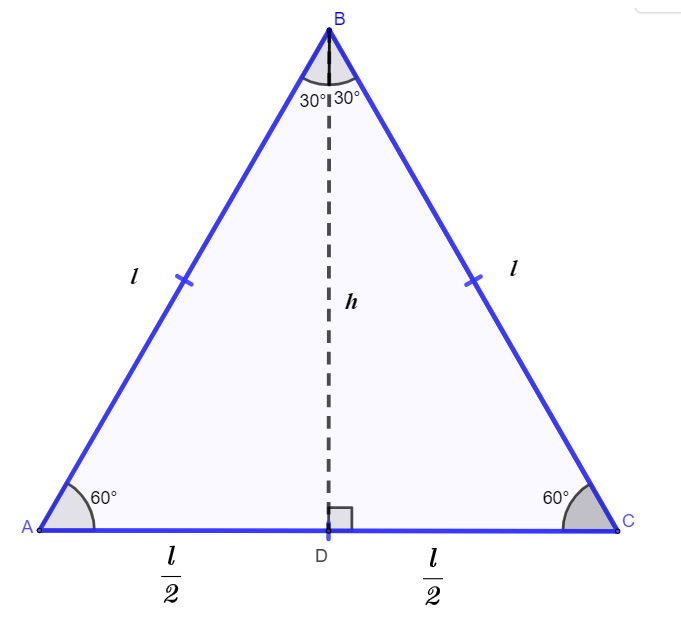
A divisão do triângulo equilátero em dois triângulos retângulos ocorre como consequência de quando traçamos a sua altura. Analisando a imagem anterior, podemos aplicar o teorema de Pitágoras no triângulo ABD para encontrar uma fórmula que nos dê a altura do triângulo de acordo com o comprimento do seu lado:
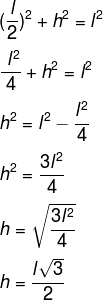
Então, como fórmula exclusiva para calcular a altura de um triângulo equilátero, temos:
![]()
Área do triângulo equilátero
A área do triângulo equilátero também possui uma fórmula específica para ser calculada. Sabemos que a área de qualquer triângulo é igual ao produto entre a base e a altura dividido por 2. Contudo, se substituirmos a altura pela fórmula encontrada anteriormente, encontraremos uma fórmula para a área do triângulo equilátero que depende somente do comprimento do seu lado.
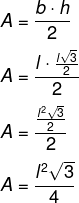
Então, para calcular a área de um triângulo equilátero, podemos utilizar a fórmula:
![]()
-
Videoaula sobre área do triângulo equilátero
Perímetro do triângulo equilátero
Assim como os outros polígonos, o perímetro de um triângulo equilátero é igual à soma dos seus lados. Como os três lados de um triângulo equilátero são congruentes, com comprimento igual a l, então, o seu perímetro é dado pela fórmula:
P = 3l
Assim, se o comprimento do lado de um triângulo equilátero for conhecido, para encontrar o seu perímetro, basta multiplicar esse comprimento por 3.
Tipos de triângulo
Quando analisamos as medidas dos lados dos triângulos, existem outras duas classificações possíveis além do triângulo equilátero. Nesse sentido, podemos ter dois lados congruentes, e quando é esse o caso, temos o triângulo isósceles. O outro caso possível é quando o triângulo não possui nenhum lado congruente, o que configura o triângulo escaleno.
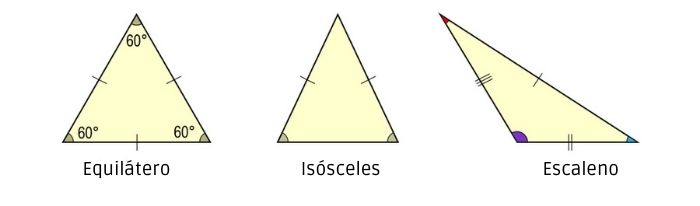
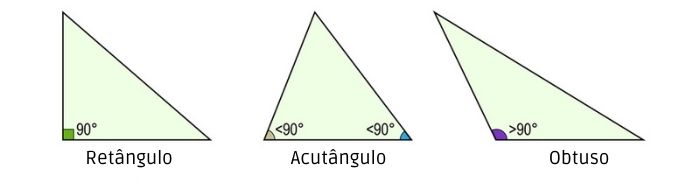
Existe uma segunda maneira de classificar os triângulos, que é analisando os seus ângulos internos. Nesse caso, as classificações são: triângulo acutângulo, quando todos os ângulos internos são agudos; triângulo retângulo, quando há um ângulo interno reto; triângulo obtuso, quando há um ângulo interno obtuso.
Exercícios resolvidos sobre triângulo equilátero
Questão 1
Para realizar o cultivo de determinada cultura, foi separado um terreno no formato de um triângulo equilátero cujas medidas dos lados eram desconhecidas.
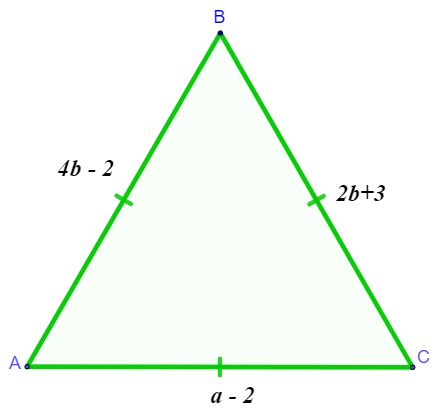
Analisando os lados do triângulo, podemos afirmar que o valor de a – b é:
A) 2,5
B) 4,5
C) 5,0
D) 7,5
E) 10
Resolução:
Alternativa D
Primeiro, vamos igualar os lados que possuem a incógnita b.
4b – 2 = 2b + 3
4b – 2b = 3 + 2
2b = 5
b = 5 : 2
b = 2,5
Sabendo que b = 2,5, temos que:
2b + 3 = a – 2
2(2,5) + 3 = a – 2
5 + 3 = a – 2
8 = a – 2
a = 8 + 2
a = 10
Então:
a – b = 10 – 2,5 = 7,5
Questão 2
(Vunesp) O quadrado da altura de um triângulo equilátero é exatamente 300. O perímetro desse triângulo, em determinada unidade de medida, é:
A) 60
B) 50
C) 30
D) 20
E) 10
Resolução:
Alternativa A
Foi dado que a altura ao quadrado do triângulo é igual a 300, ou seja, h² = 300, então, temos que:
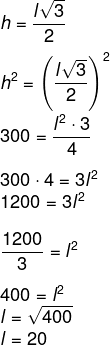
Como o lado mede 20, então, para calcular o perímetro do triângulo, basta multiplicar 20 por 3:
P = 3l
P = 3 · 20
P = 60