Relações métricas na circunferência: relação entre cordas

Relações métricas são propriedades que possibilitam o cálculo de medidas de comprimento de algumas figuras geométricas e de seus elementos. Assim, a partir da relação entre cordas de uma circunferência, é possível encontrar algumas medidas do comprimento dessas cordas por meio de uma propriedade bem definida com cálculo simples.
Para facilitar a compreensão dos cálculos, relembraremos, primeiro, as definições básicas de circunferência e corda.
Definição de circunferência e de corda
Para dado ponto O, chamado centro, a circunferência de raio r é o conjunto de pontos cuja distância até o ponto O é igual a r. Um de seus elementos é a corda, definida como segmento de reta que liga dois pontos pertencentes a uma circunferência. Assim, um diâmetro fica definido como a maior corda que uma circunferência possui, ou como a corda que passa pelo centro dela.
Cordas no interior de uma circunferência
Relação entre cordas
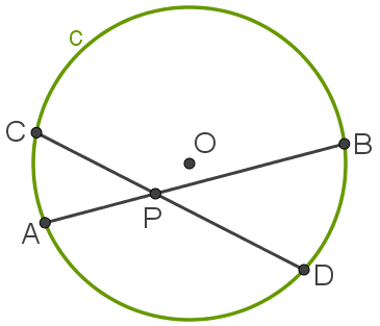
Na imagem a seguir, observe a circunferência c, de raio r e centro O. Nessa figura, construímos duas cordas, o segmento AB e o segmento CD, que se encontram no ponto P.
Nessas circunstâncias, os segmentos formados pelas cordas são proporcionais conforme a igualdade:
AP = CP
DP BP
Usando a propriedade fundamental das proporções, temos:
AP·BP = CP·DP
Essas igualdades podem ser usadas para encontrar a medida de um dos quatro segmentos de reta definidos pelas cordas da circunferência quando as medidas dos outros três são conhecidas.
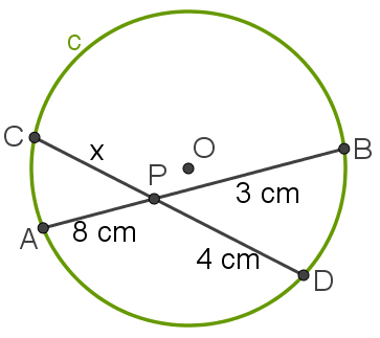
Exemplo: Determine o valor de x na imagem abaixo:
Solução: Basta usar uma das igualdades dadas acima para descobrir o valor de x.
AP·BP = CP·DP
8·3 = x·4
24 = x
4
x = 6
Demonstração da proporcionalidade das cordas
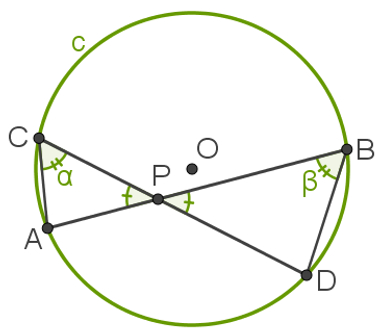
Dada a circunferência c, cortada pelas cordas AB e CD que se cruzam no ponto P, temos a formação de alguns ângulos, como mostra a seguinte imagem:
Observe que construímos também os segmentos AC e BD para formar dois triângulos dentro da circunferência: ACP e BDP. Os ângulos formados no ponto P em destaque na figura são opostos pelo vértice, por isso, suas medidas são iguais.
Os ângulos α e β também são congruentes. Isso acontece porque eles são ângulos inscritos da circunferência e relacionam-se ao mesmo arco.
Como os dois triângulos possuem dois ângulos congruentes, então, essas figuras são semelhantes pelo caso de semelhança ângulo-ângulo. É por esse motivo que os lados desses triângulos são proporcionais.
Artigos Relacionados

Últimas notícias
Outras matérias