Retas perpendiculares
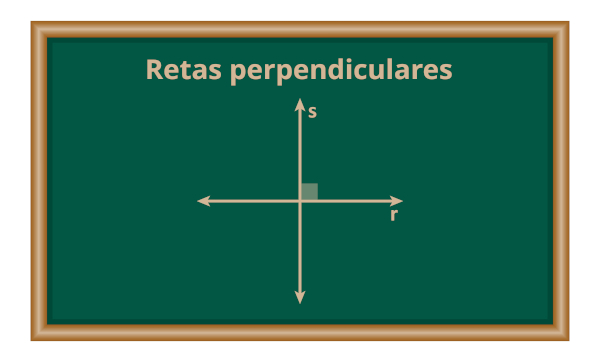
Retas perpendiculares são duas retas cujo ângulo entre elas mede 90°. Se r e s são retas perpendiculares, então escrevemos \(r⊥s\). Podemos identificar duas retas perpendiculares a partir de suas equações reduzidas, que apresentam o formato \(y=mx+n\). Se \(m_r\) é o coeficiente angular de r e \(m_s\) é o coeficiente angular de s, então \(m_r⋅m_s=-1\).
Leia também: Plano cartesiano — para que serve e como se faz
Resumo sobre retas perpendiculares
-
Duas retas são perpendiculares se o ângulo entre elas é reto, ou seja, mede 90°.
-
Escrevemos \(r⊥s\) para denotar que r é perpendicular a s.
-
Se r e s são retas perpendiculares, então vale a seguinte relação entre os coeficientes angulares de r \((m_r)\) e de s \((m_s)\):
\(m_r=-\frac{1}{m_s }\)
-
Se r e s são retas perpendiculares, \(a_r x+b_r y=c_r\) é a equação geral da reta r, e \(a_s x+b_s y=c_s \) é a equação geral da reta s, então
\(a_r⋅a_s+b_r⋅b_s=0\)
O que são retas perpendiculares?
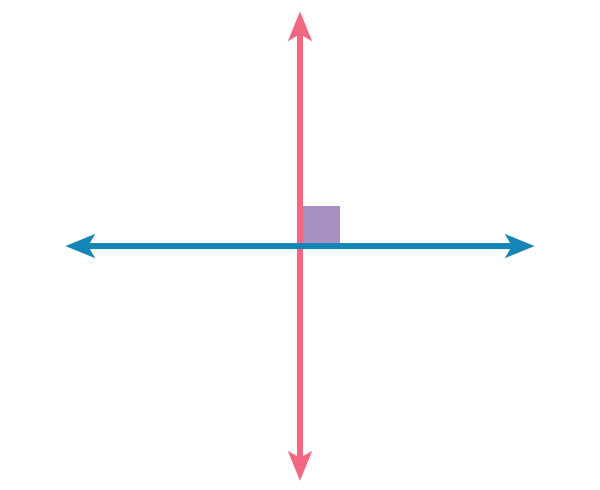
Considere que as retas r e s estão contidas em um mesmo plano e se cruzam, ou seja, são concorrentes. Dizemos que r e s são perpendiculares se o ângulo entre elas é 90°. Notação: \(r⊥s\) (lê-se “r é perpendicular a s”). Na representação gráfica, o ângulo reto é indicado por um pequeno quadrado.
Quais são as propriedades das retas perpendiculares?
-
Propriedade 1: Como as retas perpendiculares são um caso particular de retas concorrentes, então por duas retas perpendiculares passa um único plano. Em outras palavras, dadas duas retas perpendiculares, existe apenas um plano que as contém.
-
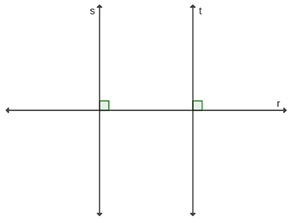
Propriedade 2: Suponha que r, s e t são retas tais que r é perpendicular a s, e r é perpendicular a t. Então, s e t são retas paralelas, ou seja, são retas que não possuem pontos em comum.
Coeficiente angular de retas perpendiculares
Considere \(y_r=m_r⋅x+n_r\) a equação reduzida da reta r e \(y_s=m_s⋅x+n_s\) a equação reduzida da reta s. Assim, mr e ms são os coeficientes angulares das retas r e s, respectivamente.
Analisando a relação entre \(m_r\) e \(m_r\), podemos determinar se as retas r e s são perpendiculares ou não. Se r e s são retas perpendiculares, então
\(m_r=-\frac{1}{m_s }\)
Ou, de forma equivalente,
\(m_r⋅m_s=-1\)
Veja também: Como calcular a distância entre dois pontos
Como identificar duas retas perpendiculares entre si?
Vejamos como identificar duas retas perpendiculares entre si a partir de suas equações reduzidas.
Exemplo 1:
As retas \(r: y=x-3\) e \(s: y=-x + 7\) são perpendiculares?
Note que \(m_r=1\) e \(m_s=-1\) e
\(m_r⋅m_s=1⋅(-1)=-1\)
Portanto, as retas r e s são perpendiculares.
Exemplo 2:
As retas \(r: y=3x-7\) e \( s: -6x+47 \) são perpendiculares?
Observe que \(m_r=3\) e \(m_s=-6\) e
\(m_r⋅m_s=3⋅(-6)=-18\)
Portanto, as retas r e s não são perpendiculares.
Método prático para identificar retas perpendiculares
Outro modo de identificar se duas retas são perpendiculares entre si é verificar a relação entre os coeficientes das equações gerais. Considere \(a_r x+b_r y=c_r\) a equação geral da reta r e \(a_s x+b_s y=c_s\) a equação geral da reta s. Se r e s são retas perpendiculares, então
\(a_r⋅a_s+b_r⋅b_s=0\)
Exemplo:
As retas \( r: 5x+2y=14 \) e \(s: -2x+5y=-43\) são perpendiculares?
Perceba que \( a_r=5\), \(a_s=-2\), \(b_r=2 \) e \(b_s=5\) e
\(a_r⋅a_s+b_r⋅b_s=5⋅(-2)+2⋅5 = -10 + 10=0\)
Portanto, as retas r e s são perpendiculares.
Saiba mais: Retas paralelas cortadas por uma transversal — ângulos e propriedades
Posições relativas entre retas
Considere que as retas r e s são distintas e estão contidas em um mesmo plano. Assim, r e s podem ser retas concorrentes ou paralelas.
-
Retas concorrentes: r e s são concorrentes se possuem um ponto de intersecção. Se o ângulo entre r e s é 90°, as retas são perpendiculares.
-
Retas paralelas: r e s são paralelas se não possuem nenhum ponto em comum.
Observação: duas retas que possuem todos os pontos em comum são chamadas de paralelas coincidentes ou apenas coincidentes.
Exercícios resolvidos sobre retas perpendiculares
Questão 1
Qual deve ser o valor de k para que as retas \(r:y=2x-2\) e \(s:y=kx+3 \) sejam perpendiculares?
a) \(-\frac{1}2\)
b) \(-\frac{1}3\)
c) 1
d) 13
e) 12
Resolução
Note que k é o coeficiente angular da reta s e 2 é o coeficiente angular da reta r. Assim, para que r e s sejam perpendiculares,
\(m_s=-\frac{1}{m_r }\)
\(k=-\frac{1}2\)
Alternativa A.
Questão 2
(Ufam – adaptado) Considere as retas \(r: -x+2y=10\) e \(s:2x+y=5\). É correto afirmar que
a) as retas são paralelas.
b) as retas são perpendiculares.
c) as retas são concorrentes no ponto (5,0).
d) as retas são concorrentes no ponto (-10,0).
e) as retas são coincidentes.
Resolução
Note que o problema informa as equações gerais das retas r e s, em que \(a_r=-1\), \(a_s=2\), \(b_r=2 \) e \(b_s=1\). Assim,
\(a_r⋅a_s+b_r⋅b_s=(-1)⋅2+2⋅1=-2+2=0\)
Logo, r e s são retas perpendiculares.
Alternativa B.
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.
Artigos Relacionados

Últimas notícias
Outras matérias


















