Teorema da bissetriz interna
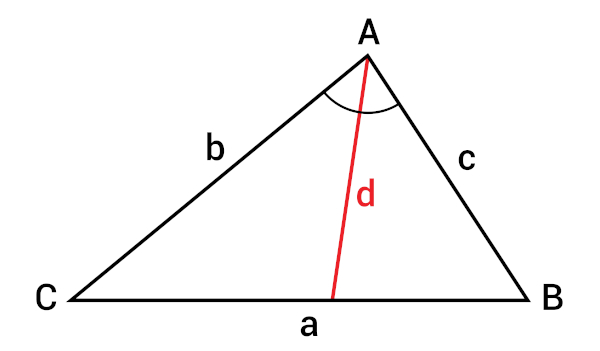
O teorema da bissetriz interna é aplicado em triângulos. Por meio dele, é possível demonstrar que ao traçar qualquer uma das bissetrizes internas desse polígono, elas dividirão o lado oposto em segmentos de reta que são proporcionais a seus lados adjacentes.
A partir do teorema da bissetriz interna é possível encontrar valores desconhecidos em um triângulo. Existe também o teorema da bissetriz externa. Como o nome sugere, ele está relacionado ao ângulo externo do triângulo.
Leia também: Quais são os pontos notáveis de um triângulo?
Resumo sobre teorema da bissetriz interna
-
O teorema da bissetriz interna é aplicado em triângulos.
-
Ele mostra que a bissetriz de um ângulo interno do triângulo divide o lado em segmentos proporcionais aos lados adjacentes.
-
Existe também o teorema da bissetriz externa, que mostra proporções parecidas relacionadas à bissetriz do ângulo externo do triângulo.
Videoaula sobre teorema da bissetriz interna
O que é uma bissetriz?
Para compreender o teorema, é importante compreender o que é a bissetriz, definida pela semirreta que divide um ângulo em duas partes congruentes.
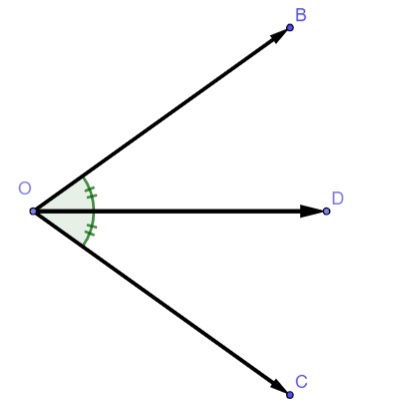
Quando a bissetriz de um triângulo é delineada, a ideia é a mesma. A bissetriz de um ângulo interno do triângulo é um segmento de reta que divide aquele ao meio.
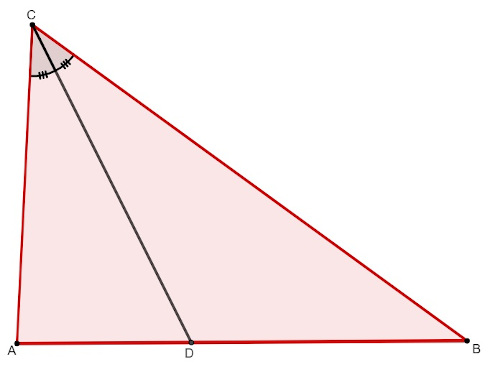
Note que, além de dividir o ângulo ao meio, a bissetriz divide a base do triângulo em dois segmentos, AD e DB. O teorema abordado a seguir mostra uma relação de proporcionalidade entre os segmentos e os lados AC e BC.
Leia também: Segmentos proporcionais — aqueles que apresentam relações de proporcionalidade entre si
Como é o teorema da bissetriz interna?
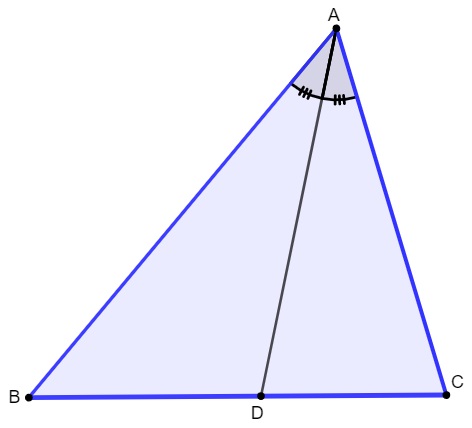
O teorema da bissetriz interna mostra que se traçarmos a bissetriz AD em um triângulo de lados ABC, encontraremos dois segmentos. A razão entre o lado AC e o segmento CD é igual à razão entre o lado AB e o segmento BD.
![]()
Demonstração do teorema da bissetriz interna
Dado o triângulo ABC, com bissetriz AD, delimitaremos o prolongamento do lado AB e um segmento CE paralelo à bissetriz do triângulo, como na imagem abaixo:
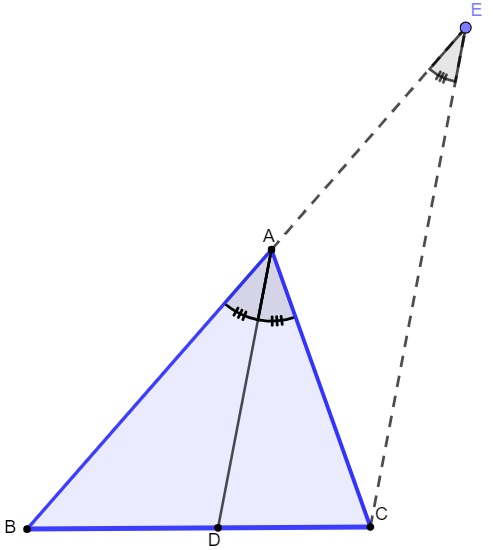
Pelo teorema de Tales, sabemos que a reta transversal forma segmentos proporcionais, então temos o seguinte:
![]()
Sendo x o ângulo conhecido, qual o valor dos ângulos internos do triângulo AEC?
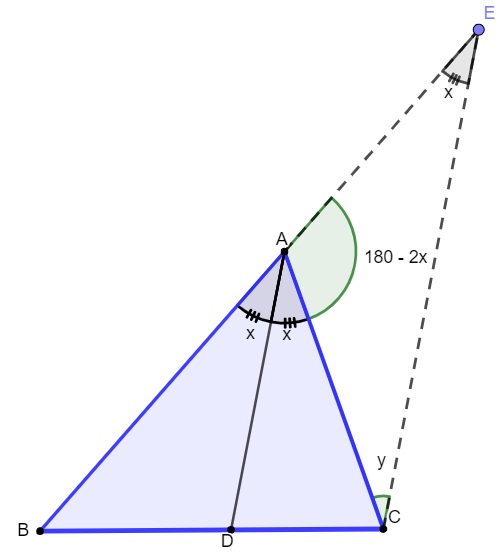
A soma dos ângulos internos de um triângulo é sempre igual a 180°. Dessa forma, no triângulo ACE, calcula-se:
x + 180º – 2x + y = 180º
– x + y = 180° – 180°
– x + y = 0
y = x
Se o ângulo x e o ângulo y possuem a mesma medida, o triângulo ACE é isósceles. Logo, os segmentos AE e AC são congruentes. Trocando AE por AC na razão, fica provado que:
![]()
Exemplo:
Dado o triângulo a seguir, encontre o valor de x.
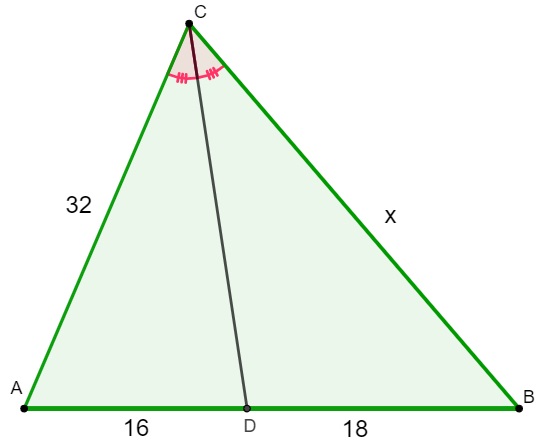
Resolução:
Analisando a imagem, nota-se que basta aplicar o teorema da bissetriz interna nesse triângulo. Montando as proporções, temos que:
![]()
Multiplicando de forma cruzada, calcula-se:
16x = 32 · 18
16x = 576
x = 576 : 16
x = 36
Diferença entre o teorema da bissetriz interna e o teorema da bissetriz externa
O teorema da bissetriz interna não é o único teorema envolvendo a bissetriz de um triângulo. Além dele, existe o teorema da bissetriz externa. Como o nome sugere, o teorema da bissetriz externa está ligado à bissetriz de um ângulo externo, diferentemente do teorema da bissetriz interna, que utiliza apenas os ângulos internos do triângulo.
Ambos os teoremas nos auxiliam a encontrar valores desconhecidos por meio da proporção. Assim, utilizamos o teorema que for mais conveniente de acordo com as informações já conhecidas.
Leia também: Congruência de triângulos — os casos em que eles apresentam medidas iguais
Exercícios resolvidos sobre teorema da bissetriz interna
Questão 1
Analisando o triângulo a seguir, podemos afirmar que o comprimento do lado AB é igual a
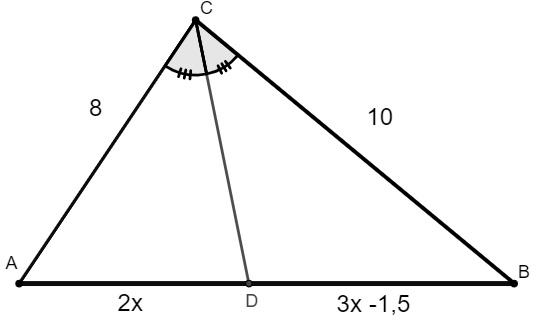
A) 15,0
B) 14,8
C) 13,5
D) 7,5
E) 6
Resolução:
Alternativa C
Sabemos que os segmentos são proporcionais. Portanto, montaremos a proporção e multiplicaremos de forma cruzada:
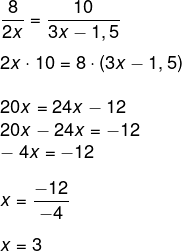
Conhecendo o valor de x, sabemos que o lado AB é igual a 2x + 3x – 1,5. Dessa forma, obtém-se o seguinte:
AB = 2x + 3x – 1,5
AB = 5x – 1,5
Substituindo x = 3:
AB = 5 · 3 – 1,5
AB = 15 – 1,5
AB = 13,5
Questão 2
(CFTMG 2015) O perímetro do triângulo ABC vale 120 cm e a bissetriz do ângulo  divide o lado oposto em dois segmentos de 18 cm e 22 cm, conforme a figura.
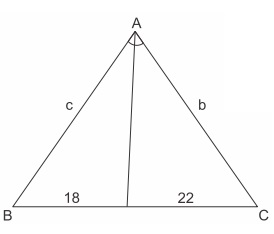
A medida do maior lado desse triângulo em centímetros é de:
A) 22
B) 36
C) 44
D) 52
Resolução:
Alternativa C
Sabemos que o perímetro do triângulo é de 120 cm, então:
c + b + 18 + 22 = 120
c + b = 120 – 40
c + b = 80
c = 80 – b
Pelo teorema da bissetriz interna, temos:
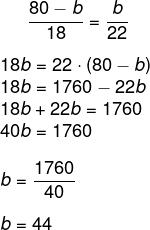
Analisando os lados, sabemos que b > c, pois:
c = 80 – b
c = 80 – 44
c = 36
Portanto, o maior lado desse triângulo mede 44 cm.
Artigos Relacionados

Últimas notícias
Outras matérias


















