Aceleração centrípeta
Aceleração centrípeta é a aceleração que causa a mudança na direção da velocidade de algum móvel que execute um movimento circular. Ela aponta na direção do raio do movimento e é calculada pela velocidade escalar do móvel elevada ao quadrado, dividida pelo raio da circunferência.
Essa aceleração surge graças à ação de uma força central, ou seja, uma força que aponta para o centro de uma trajetória. Essas forças centrais são chamadas de forças centrípetas. Uma vez que o ângulo entre a velocidade e a força centrípeta é de 90º, essa força não é capaz de realizar trabalho, por isso a aceleração centrípeta somente muda a direção do movimento, mantendo constante a velocidade em que o corpo se move.
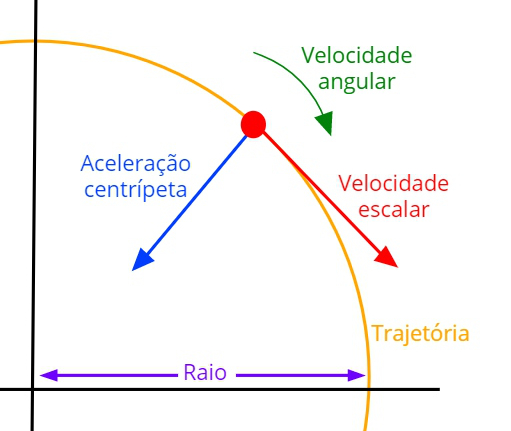
Para entendermos melhor o significado de aceleração centrípeta, vamos analisar uma de suas possíveis fórmulas:
![]()
acp – aceleração centrípeta (m/s²)
v – velocidade escalar (m/s)
ω – velocidade angular (rad/s – radianos por segundo)
De acordo com a fórmula mostrada acima, a unidade de aceleração centrípeta é o rad/s multiplicado por m/s. Porém, a unidade radiano é adimensional (não tem unidade de medida), por isso dizemos que aceleração centrípeta é medida em m/s².
Se um móvel tem aceleração centrípeta de 1 m/s², a direção de sua velocidade é alterada em 1 rad a cada segundo, percorrendo 1 metro a cada segundo.
Veja também: Tudo o que você precisa para entender o movimento circular de uma vez por todas!
Fórmula de aceleração centrípeta
A fórmula mais utilizada para o cálculo da aceleração centrípeta é aquela que relaciona o quadrado da velocidade com o raio da trajetória.
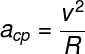
v – velocidade escalar (m/s)
R – raio da trajetória
Além da fórmula acima, existem variações que se relacionam às grandezas angulares do movimento circular, como a velocidade angular ou a aceleração angular.
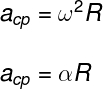
Aceleração centrífuga
Quando colocamos uma roupa molhada para secar em uma máquina de lavar roupas, a água das peças é expulsa na direção tangencial ao deslocamento. Sobre esse movimento, é comum ouvirmos que a aceleração centrípeta é a responsável por fazer as gotículas de água deixarem a roupa, entretanto, essa afirmação está errada, uma vez que a responsável pela fuga das gotículas de água é a inércia.
O uso de termos como aceleração centrífuga e força centrífuga é bastante comum e passa a ideia errada de que existe alguma força fazendo com que os corpos em rotação tendam a ser lançados para fora de sua trajetória. Essa “força” que parece impelir os corpos para direções que fogem ao centro da rotação, na verdade, surge em referenciais acelerados e, por isso, é chamada de força virtual.
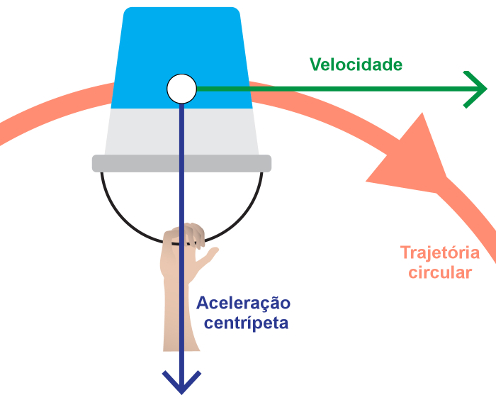
Durante o movimento de rotação, os corpos tendem a continuar movendo-se em linha reta, em velocidade constante. É por causa da inércia que podemos girar um balde cheio de água sem que o seu conteúdo caia: uma vez que a força centrípeta aponta para o centro da trajetória, a inércia da água faz com que ela tenda a se opor à ação dessa força. Quando a água do balde encontra-se perto de cair, o balde (que tem menor inércia) já desceu, desse modo, a água permanece sempre dentro do balde.
Aceleração centrípeta do elétron
Uma aplicação comum da aceleração centrípeta é aquela em que partículas carregadas são lançadas em direção a uma região de campo magnético. Quando isso acontece, uma força magnética atua sobre elas, fazendo com que a sua trajetória curve-se. Nesse caso, a força magnética faz o papel de uma força centrípeta, já que ela constantemente aponta para o centro de uma trajetória circular. Desse modo, basta assumirmos que a força magnética tem caráter centrípeto:
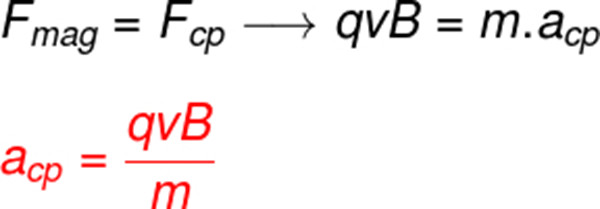
Fmag – força magnética (N - Newton)
Fcp – força centrípeta (N)
q – carga elétrica (C - Coulomb)
v – velocidade (m/s)
B – campo magnético (T)
Caso queiramos calcular a aceleração centrípeta sofrida por um elétron, devemos assumir que o módulo de q é igual ao da carga elétrica fundamental (1,6.10-19 C). Após alguns ajustes, podemos escrever uma fórmula para calcular o raio de rotação de um elétron na presença de campos magnéticos, a saber:
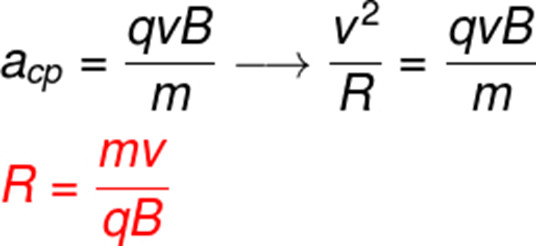
Vamos fazer um exemplo de aplicação da fórmula acima para determinar qual deve ser o raio da trajetória de um elétron de carga 1,6.10-19 C que adentra uma região de campo magnético de 0,5 T com velocidade de 1,5.103 m/s. A massa dos elétrons é de aproximadamente 9.10-31 kg. Veja o cálculo:
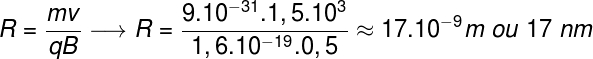
É possível que você se pergunte sobre qual é a aceleração centrípeta de um elétron que orbita o núcleo de um átomo. Apesar de pertinente, o resultado desse cálculo nos leva a inconsistências físicas e isso ocorre por causa do modelo atômico utilizado. Se esses elétrons estivessem de fato girando, estariam emitindo energia constantemente, de modo que suas órbitas seriam instáveis. Hoje em dia sabemos que os elétrons não orbitam os núcleos atômicos, mas que eles se distribuem no volume da eletrosfera de acordo com leis muito mais complexas, fundamentadas nos princípios da mecânica quântica.

Exercícios sobre aceleração centrípeta
Questão 1 - (Enem 2019) O Brasil pode se transformar no primeiro país das Américas a entrar no seleto grupo das nações que dispõem de trens-bala. O Ministério dos Transportes prevê o lançamento do edital de licitação internacional para a construção da ferrovia de alta velocidade Rio-São Paulo. A viagem ligará os 403 quilômetros entre a Central do Brasil, no Rio, e a Estação da Luz, no centro da capital paulista, em 1 hora e 25 minutos.
Devido à alta velocidade, um dos problemas a serem enfrentados na escolha do trajeto que será percorrido pelo trem é o dimensionamento das curvas. Considerando-se que uma aceleração lateral confortável para os passageiros e segura para o trem seja de 0,1 g, em que g é a aceleração da gravidade (considerada igual a 10 m/s2) e que a velocidade do trem mantenha-se constante em todo o percurso, seria correto prever que as curvas existentes no trajeto deveriam ter raio de curvatura minimo de, aproximadamente:
a) 80 m
b) 430 m
c) 800 m
d) 1600 m
e) 6400 m
Gabarito: Letra E
Resolução:
Pede-se que encontremos o raio mínimo da curva que o trem precisa percorrer para que os passageiros não se sintam desconfortáveis. Para isso, devemos calcular a velocidade escalar do trem:

Questão 2 - Um carro de fórmula 1 entra em uma curva a 108 km/h (30 m/s). Sabendo que o raio da curva em questão é de 90,0 m, a aceleração centrípeta sentida pelo piloto é igual a:
a) 5 m/s²
b) 10 m/s²
c) 3 m/s²
d) 8 m/s²
e) 3 m/s²
Gabarito: Letra B
Resolução:
Para fazermos o cálculo, utilizamos a fórmula da aceleração centrípeta. Confira:
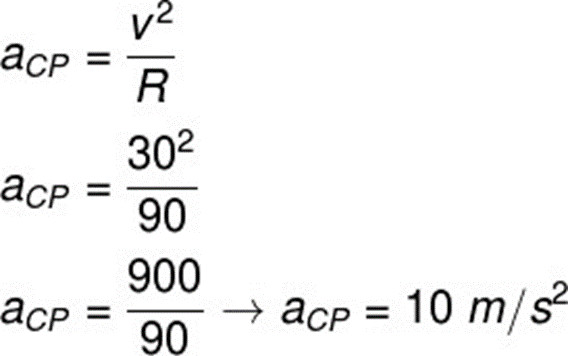
De acordo com os cálculos realizados, a aceleração centrípeta percebida pelo piloto é de 10 m/s², o equivalente a 1g (10 m/s², o módulo da aceleração da gravidade).
Artigos Relacionados

Últimas notícias
Outras matérias


















