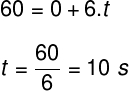Diagrama horário do MUV

Quando um corpo tem sua velocidade alterada de maneira constante, dizemos que se encontra em movimento uniformemente variado (MUV).

Os diagramas horários do movimento uniformemente variado (MUV) são gráficos que relacionam grandezas, como posição, velocidade e aceleração, com a passagem do tempo. Por meio dos diagramas do MUV, podemos calcular a velocidade do móvel, seu deslocamento e, até mesmo, suas variações de velocidade.

Gráfico de velocidade por tempo (v x t) no MUV

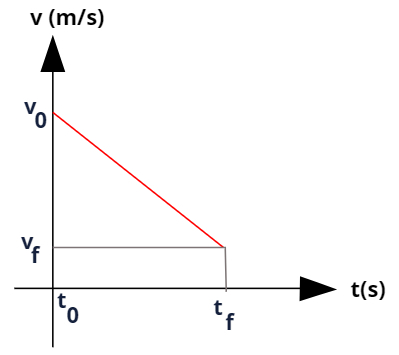
O gráfico da velocidade em função do tempo no movimento uniformemente variado é sempre uma reta ascendente ou descendente, uma vez que a velocidade nesse tipo de movimento está sujeita a uma aceleração ou desaceleração de módulo constante.

Quando a velocidade de um móvel aumenta em função do tempo, ela é representada como uma reta ascendente. Esse movimento é chamado de movimento acelerado.

A fórmula usada para construir os gráficos de v(t) (velocidade em função do tempo) é chamada de função horária da velocidade. Essa função é mostrada abaixo:

Legenda:
v_f – velocidade final (m/s)
v₀ – velocidade inicial (m/s)
a – aceleração média (m/s²)
t – intervalo de tempo (s)

A função acima é uma função do 1º grau (reta). Portanto, para valores positivos de aceleração, seu gráfico será uma reta ascendente, como mostrado abaixo:

Se a velocidade do móvel decresce em função do tempo, dizemos que seu movimento é retardado. Nesse caso, o diagrama da velocidade em função do tempo também será uma reta, mas essa reta será descendente em virtude da aceleração negativa.

Além disso, esse tipo de gráfico é especialmente útil para calcular o deslocamento sofrido pelo móvel. Para tanto, basta calcular a área desse gráfico.

No gráfico acima, apesar de o módulo da velocidade ser decrescente, ela ainda está localizada acima do eixo das abscissas (eixo do tempo). Isso indica que o móvel ainda se afasta da origem. Trata-se, portanto, de um movimento progressivo retardado.

Veja também: Conceitos fundamentais da Cinemática Escalar

Gráfico de posição por tempo (S x t) no MUV

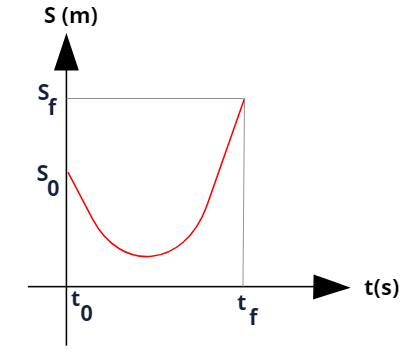
O diagrama da posição em função do tempo para o MUV é descrito pelo gráfico de uma função de segundo grau chamada de função horária da posição do MUV. Essa função pode ser escrita de duas formas:

Legenda:
S_f – posição final (m)
S_{0 –}posição inicial (m)
ΔS = S_f - S₀ – deslocamento (m)
v_f – velocidade final (m/s)
v₀ – velocidade inicial (m/s)
a – aceleração média (m/s²)
t – intervalo de tempo (s)

A função horária da posição para o MUV indica que o gráfico de posição (S) em função do tempo (t) terá o formato de parábola. Quando a velocidade do móvel aumentar em função do tempo, teremos uma parábola com a concavidade voltada para cima. Observe:

Nos casos em que o movimento sofrer desaceleração, teremos um gráfico de uma parábola com a concavidade voltada para baixo. Observe:

Os pontos mais importantes dos diagramas de posição em função do tempo são suas raízes (t' e t'' ou t₀ e t_f). Esses pontos informam-nos quando o móvel passa pela origem do referencial. Além disso, para o instante de tempo inicial (t₀), é possível determinar a posição inicial (S₀) do móvel: basta olharmos em qual altura a parábola atravessa o eixo vertical durante o instante de tempo inicial.

Veja também: Equação de Torricelli

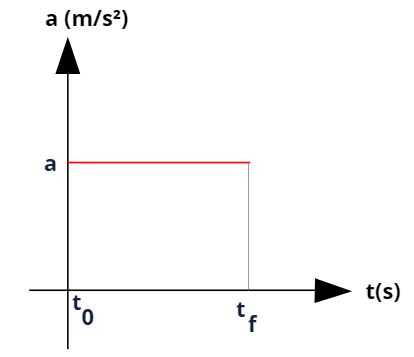
Gráfico da aceleração em função do tempo (a x t) no MUV

Os gráficos da aceleração em função do tempo são especialmente úteis para determinarmos se um corpo está sendo acelerado ou desacelerado. Por meio desses gráficos, é possível calcular a variação da velocidade sofrida pelo móvel (Δv = v_f – v₀).

Para o movimento uniformemente acelerado, teremos uma reta paralela ao eixo horizontal de altura constate. Observe:

Como a reta da aceleração está acima do eixo horizontal, dizemos que o movimento é acelerado. Para determinarmos a variação da velocidade do móvel, basta calcularmos a área desse gráfico.

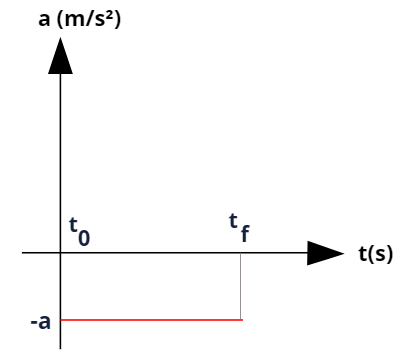
Não pare agora... Tem mais depois da publicidade ;)

Quando o móvel está sofrendo alguma desaceleração, a reta de a(t) (aceleração em função do tempo) aparecerá abaixo do eixo horizontal, pois os valores dessa reta serão negativos. Observe:

Resumo sobre o diagrama horário do MUV

→ No movimento uniformemente acelerado, o gráfico de posição em função do tempo s(t) será uma parábola com a concavidade voltada para cima, e sua aceleração será positiva.

→ No movimento uniformemente desacelerado ou retardado, o gráfico de posição em função do tempo s(t) será uma parábola com a concavidade voltada para baixo, e sua aceleração será negativa.

→ No movimento uniformemente acelerado, o gráfico da velocidade em função do tempo v(t) será uma reta ascendente (que sobe).

→ No movimento uniformemente retardado, o gráfico da velocidade em função do tempo v(t) será uma reta descendente (que desce).

→ No movimento uniformemente acelerado, o gráfico da aceleração em função do tempo a(t) será uma reta paralela ao eixo horizontal e disposta acima dele.

→ No movimento uniformemente retardado, o gráfico da aceleração em função do tempo a(t) será uma reta paralela ao eixo horizontal e disposta abaixo dele.

Exercícios resolvidos sobre gráficos do MUV

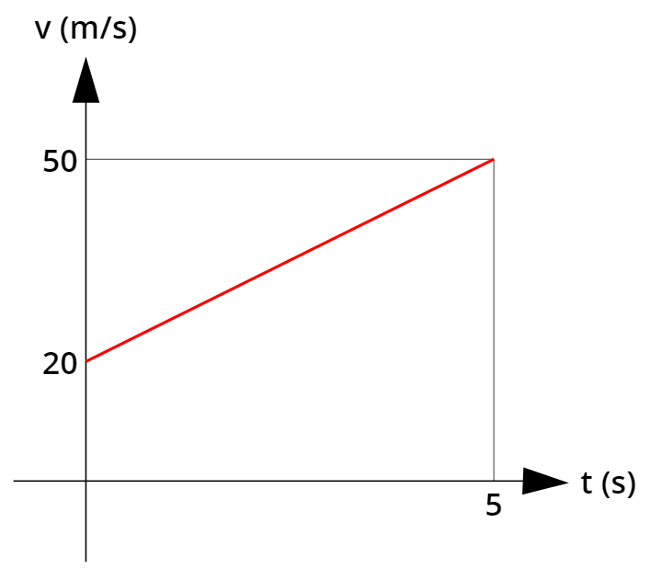
1. O gráfico da velocidade em função do tempo de um móvel que se move com aceleração constante é mostrado abaixo:

Analise o gráfico acima e responda:

a) Qual é o módulo da velocidade inicial do móvel?

b) Qual é o módulo da velocidade final do móvel?

c) Qual é o módulo da aceleração do móvel?

d) Classifique o movimento como progressivo ou regressivo, retardado ou acelerado.

e) Calcule, por meio do gráfico, o módulo do deslocamento sofrido pelo móvel.

f) Determine em qual instante a velocidade do móvel terá módulo igual a 60 m/s.

Resolução:

a) Analisando o gráfico acima, é possível perceber que, no instante de tempo inicial (t₀ = 0 s), onde se cruzam os dois eixos do gráfico, a velocidade do móvel é de 20 m/s.

b) O instante de tempo final (t_f) mostrado no gráfico é o instante t = 5 s. Nesse instante de tempo, a velocidade do móvel é de 50 m/s.

c) Podemos calcular a aceleração do móvel por meio da equação da aceleração média (equivalente à função horária da velocidade):

Analisando o gráfico, é possível encontrar os valores de v_f, v_i, t_f e t_i.Dessa forma:

O cálculo indica que a velocidade do móvel aumenta, em módulo, 6 metros por segundo a cada segundo.

d) A reta da velocidade encontra-se acima do eixo horizontal, portanto, o movimento é progressivo, ou seja, o móvel afasta-se do referencial. Além disso, a reta está inclinada para cima, indicando que seu módulo aumenta. Trata-se, portanto, de um movimento acelerado. Logo, dizemos que o movimento é progressivo e acelerado.

e) Para calcularmos a distância percorrida pelo móvel por meio do gráfico, devemos calcular a área. O gráfico tem a forma geométrica de um trapézio, cuja área é dada pela fórmula:

Legenda:
A – área do trapézio
B – aresta da base maior
b – aresta da base menor
h – altura do trapézio

Podemos assimilar a velocidade v_f à base maior B, a velocidade inicial v_i à base menor b, o instante de tempo final t_f à altura h do trapézio. Com isso, teremos:

f) Para determinarmos a velocidade do móvel em algum instante posterior àqueles apresentados no gráfico, utilizamos a função horária da velocidade:

Como calculada anteriormente, a aceleração desse móvel é igual a 6 m/s². Para que ele atinja uma velocidade final de 60 m/s, teremos a seguinte resolução: