Energia potencial elástica

Energia potencial elástica é a forma de energia que é adquirida por corpos elásticos capazes de retornarem ao seu formato original após sofrerem algum tipo de deformação. A energia potencial elástica depende da constante elástica do corpo, bem como do tamanho da deformação sofrida por ele.
Veja também: Confira as principais fórmulas de Física do Enem
Quando aplicamos força em corpos elásticos, eles se deformam, passando a estocar energia potencial elástica. Caso cesse a força, a energia potencial elástica será convertida em energia cinética. Nesse caso, dizemos que houve realização de trabalho pela força elástica.
Existem diversos objetos cotidianos que são capazes de armazenar energia potencial elástica, confira alguns deles:
-
Molas: alguns amortecedores de veículos, molas de colchões etc;
-
Látex: tiras de borracha, trampolim, bola de borracha etc.
Quer sejam comprimidos, quer sejam esticados, os corpos elásticos armazenarão energia potencial elástica. Tal energia surge quando esses corpos não assumem tamanhos diferentes daqueles que teriam caso não estivessem sob a ação de nenhuma força.
Quando comprimimos a mola, ela ganha energia potencial elástica e produz uma força contrária à compressão.
Aplicações
A maior parte das aplicações da energia potencial elástica diz respeito ao armazenamento ou conversão da energia cinética por objetos elásticos. Um bom exemplo disso são os amortecedores e os para-choques de veículos.
Os para-choques são feitos de materiais que se deformam quando ocorre alguma colisão. Dessa forma, a energia cinética do veículo pode ser absorvida, diminuindo os efeitos aos passageiros dos veículos.

Os para-choques são elásticos e, por isso, conseguem transformar energia cinética em energia elástica.
Fórmula
A fórmula usada para calcular a energia potencial elástica de um corpo relaciona a sua constante elástica (k) com a deformação sofrida pelo corpo (x), e é mostrada a seguir, confira:
![]()
Ep — Energia potencial elástica (J - Joules)
k — Constante elástica (N/m)
x — Deformação do objeto (m)
Vamos analisar a fórmula e cada uma de suas variáveis:
-
Ep: é a medida da quantidade de energia que é armazenada por algum corpo elástico que estiver sob o efeito de uma força que o deforma, essa energia é medida em Joules;
-
k: é uma propriedade de cada material. Os materiais que apresentam constante elástica elevada são geralmente mais duros, pois precisam receber uma grande intensidade de força para sofrer alguma deformação. Os materiais com baixas constantes elásticas, por sua vez, são facilmente deformados. A constante elástica é expressa em Newton por metro (N/m).
-
x: é a medida da deformação sofrida pelo corpo. Por exemplo, se uma mola tinha inicialmente um tamanho de 20 cm e é esticada até 25 cm, então a sua deformação será de 5 cm. A unidade de medida da deformação x, entretanto, deve sempre ser o metro (m). Por isso, caso fossemos fazer um cálculo com a deformação de 5 cm, deveríamos usar o valor de 0,05 m. Além disso, é importante lembrar que, caso o corpo tenha o seu comprimento aumentado, x terá sinal positivo, no entanto, caso o seu comprimento seja diminuído, o sinal de x deverá ser negativo.
Veja também: Saiba tudo sobre a primeira lei de Newton
Dedução
A energia potencial elástica é deduzida com base na lei de Hooke, que mede a intensidade da força elástica produzida por corpos deformados, juntamente à definição física de trabalho mecânico:
A lei de Hooke afirma que a força elástica surge em reação à compressão ou ao tensionamento de corpos elásticos. Trata-se de uma força de reação que sempre surge na mesma direção da ação, porém em sentido oposto:
![]()
Observe a próxima figura, nela temos uma mola em seu formato original, em seguida, uma força externa (Fext) estica-a, fazendo com que ela passe a exercer uma força elástica no sentido oposto:
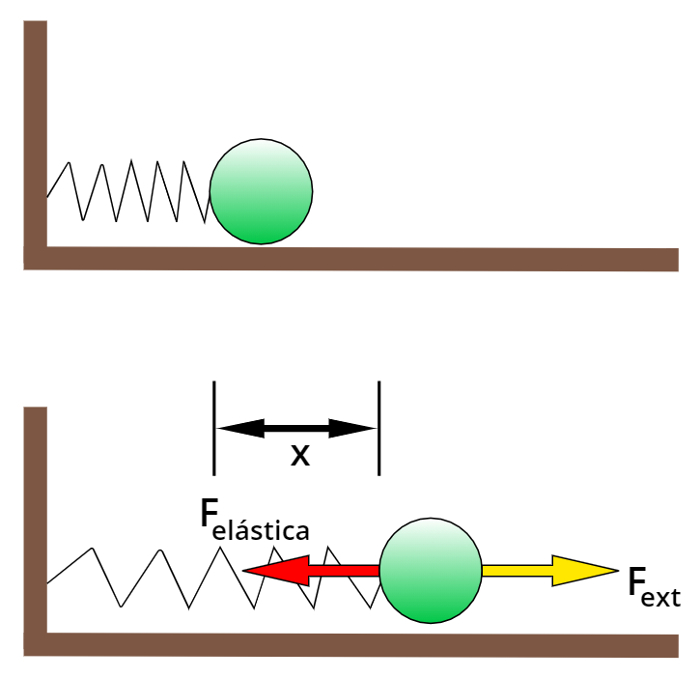
A quantidade de energia que foi gasta para esticar essa mola é correspondente ao trabalho que precisou ser realizado sobre ela. Observando a fórmula da lei de Hooke, quanto maior for a elongação da mola, maior será a força elástica que ela exerce. Por isso, a fim de calcularmos o trabalho realizado pela força elástica, faremos o gráfico de força em função da distância:
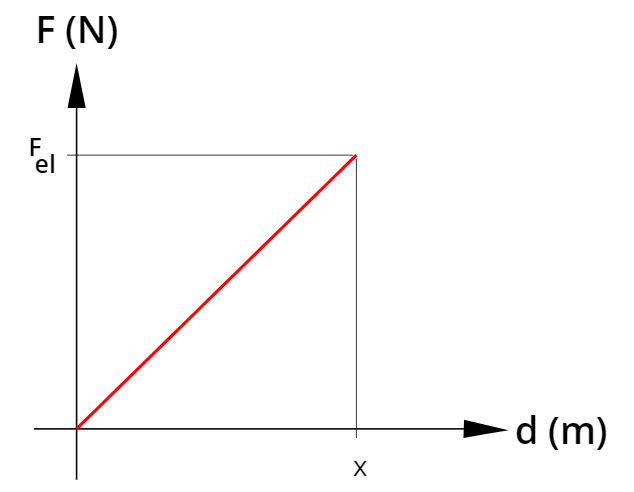
Fel — Força elástica
Para calcularmos o trabalho que foi realizado no gráfico acima, é necessário calcular a sua área, que é triangular. Observe que a base desse triângulo tem módulo x, enquanto sua altura é determinada pelo módulo da força elástica (Fel = kx). Confira o cálculo:
![]()
De acordo com esse cálculo, o trabalho necessário para deformar a mola é dado pelo produto da constante elástica (k) pelo quadrado da deformação dividido por 2. Essa quantidade de trabalho é exatamente a quantidade de energia que é armazenada pela mola em forma de energia potencial elástica.
Exercícios resolvidos
Questão 1) Uma mola de constante elástica igual a 20 N/m é esticada, e seu comprimento, que era inicialmente de 20 cm, passa a ser de 50 cm. Qual é o módulo da energia potencial elástica armazenada nessa mola?
a) 30 J
b) 200 J
c) 0,9 J
d) 50 J
e) 250 J
Gabarito: Letra C
Resolução:
A energia potencial elástica pode ser calculada por meio desta fórmula:
![]()
Entretanto, para usá-la, precisamos conferir se todas as unidades fornecidas pelo exercício encontram-se compatíveis. Dessa forma, percebe-se que os tamanhos inicial e final da mola estão fornecidos na unidade de centímetros (cm), por isso precisamos que essa seja expressa em metros. A deformação x é a diferença entre os comprimentos final e inicial, ou seja, equivale a 30 cm (0,3 m). Confira o cálculo:
![]()
Questão 2) Uma mola é comprimida por uma força de 200 N e tem o seu comprimento reduzido em 50 cm. Qual é a energia potencial elástica adquirida pela mola?
a) 50 000 J
b) 25 000 J
c) 500 J
d) 50 J
e) 1 200 J
Gabarito: Letra D
Resolução:
O exercício pede que encontremos a energia potencial elástica, no entanto, não nos informa quanto vale a constante elástica da mola para que possamos calculá-la. Para isso, teremos que usar a lei de Hooke e, em seguida, calcularmos a energia potencial elástica, confira:
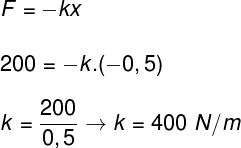
Após conhecermos o módulo da constante elástica da mola, podemos calcular a sua energia potencial elástica:
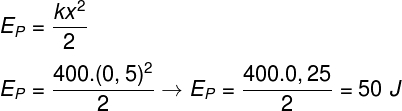
Artigos Relacionados

Últimas notícias
Outras matérias


















