Energia potencial elétrica
Energia potencial elétrica é uma forma de energia relacionada à posição relativa entre pares de cargas elétricas. A energia potencial elétrica é uma grandeza escalar, medida em joules, que pode ser calculada multiplicando-se o módulo da carga de prova, medida em coulombs, pelo potencial elétrico, em volts.
Veja mais: Potencial elétrico em um ponto p
Definição de energia potencial elétrica
Toda carga elétrica produz um campo elétrico que se permeia pelo espaço, sendo capaz de produzir forças de atração ou repulsão sobre outras cargas elétricas. A interação entre cargas, portanto, dá origem a uma energia potencial, que pode ser transformada em energia cinética, no caso em que uma dessas cargas seja móvel, por exemplo.
Sozinha, uma carga elétrica não apresenta energia potencial elétrica, é preciso que uma carga de prova interaja com ela, dessa maneira, a medida da energia potencial elétrica depende da magnitude das cargas, bem como da distância entre elas.
A energia potencial elétrica é uma grandeza escalar, e, por isso, para conhecermos a medida da energia potencial elétrica total de um sistema de vários corpos carregados, é necessário somar a energia potencial gerada pela interação de cada par de corpos eletrizados.
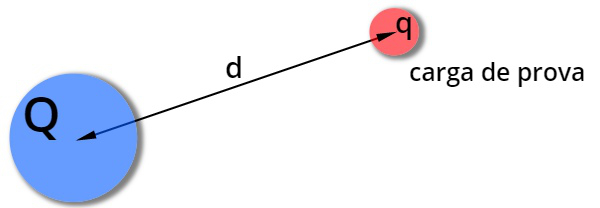
Fórmula de energia potencial elétrica
A fórmula de energia potencial elétrica (EP) é dada pelo produto entre a carga elétrica geradora (Q), a carga elétrica de prova (q), e a constante eletrostática do vácuo (k0), dividido pela distância entre as cargas, como mostramos a seguir:
![]()
Além dessa fórmula, é possível calcular a energia potencial elétrica por meio do potencial elétrico produzido pela carga geradora (U) multiplicado pela magnitude da carga elétrica de prova. Ao levarmos em conta o sinal da energia potencial elétrica, entende-se que uma energia potencial elétrica negativa está relacionada à atração entre as cargas, enquanto um sinal positivo refere-se à repulsão entre as cargas.
![]()
Veja também: Equações da eletricidade
Exemplo de energia potencial elétrica
Confira um exemplo de como se deve usar a fórmula de energia potencial elétrica:
Duas cargas elétricas de 2,0 μC e -3,0 μC encontram-se fixas e separadas por uma distância de 0,5 m, no vácuo. Calcule a energia potencial elétrica gerada pela interação entre essas cargas.
Resolução:
Para resolver o exemplo, devemos lembrar-nos dos prefixos de unidades, muito comuns para a denotação de cargas elétricas, que geralmente exigem unidades de medida muito pequenas. Em seguida, sabendo que o prefixo μ equivale à 10-6, devemos desenvolver o cálculo da energia potencial elétrica:
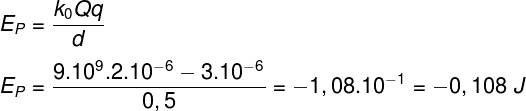
Energia potencial elétrica no capacitor
Os capacitores são dispositivos utilizados para o armazenamento de cargas elétricas, dito isso, é possível calcular a quantidade de energia potencial elétrica armazenada entre as armaduras condutoras dos capacitores. Para tanto, precisamos conhecer alguns parâmetros, como a carga elétrica armazenada, a diferença de potencial entre as placas ou, ainda, a capacitância.
A figura seguinte traz as diferentes fórmulas usadas para o cálculo da energia potencial elétrica nos capacitores:
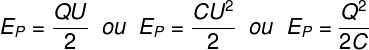
Q – carga elétrica
U – potencial elétrico
C – capacitância
Veja também: 5G - a nova rede que revolucionará as telecomunicações
Potencial elétrico e energia potencial elétrica
Potencial elétrico e energia potencial elétrica são coisas diferentes, porém relacionadas. Enquanto o potencial elétrico é medido em volts, a energia potencial elétrica é medida em joules, por exemplo. O potencial elétrico é uma propriedade de cada carga elétrica, enquanto a energia potencial elétrica é produto da interação entre pares de cargas e não existe em cargas solitárias.
A relação entre essas duas grandezas é a seguinte: o potencial elétrico é igual à energia potencial elétrica por unidade de carga, ou seja, a quantidade de volts de uma certa região do espaço determina qual será a energia potencial elétrica para cada 1 C de carga elétrica de prova.
Variação da energia potencial elétrica
A variação da energia potencial elétrica dá-se graças à realização de um trabalho pela ação da força elétrica. Quando uma carga móvel é posicionada nas proximidades de uma carga fixa, por exemplo, a força elétrica transforma a energia potencial elétrica em energia cinética, por isso, podemos dizer que a variação da energia potencial elétrica equivale ao trabalho realizado, bem como à variação da energia cinética adquirida pelas cargas móveis.
A fórmula que relaciona variação de energia potencial elétrica, trabalho e variação de energia cinética é mostrada a seguir, observe:
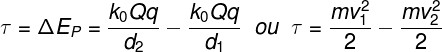
d2 e d1 – posições 1 e 2 da partícula
v1 e v2 – velocidades 1 e 2 da partícula
Veja também: O que é diferença de potencial?
Exercícios sobre energia potencial elétrica
Questão 1) Sobre a energia potencial elétrica, assinale a alternativa correta:
a) Energia potencial elétrica é a quantidade de carga elétrica armazenada em um corpo eletrizado.
b) Energia potencial elétrica é uma grandeza escalar, medida em joules.
c) Energia potencial elétrica é uma grandeza vetorial, medida em volts.
d) Energia potencial elétrica é uma medida da passagem de cargas elétricas.
e) Energia potencial elétrica é uma das formas conhecidas da energia mecânica.
Gabarito: Letra b
Resolução:
A energia potencial elétrica é uma grandeza escalar, medida em joules, sua natureza é eletromagnética, uma vez que surge da interação entre cargas elétricas, portanto, a alternativa correta é a letra b.
Questão 2) Determine a intensidade da energia potencial elétrica de um sistema composto de duas cargas fixas de 1,0 mC e 0,5 mC, e 0,25 m distantes uma da outra, e assinale a alternativa correspondente:
Use k0 = 9.109 N.m²/C²
a) 1,8.104 J
b) 2,7.104 J
c) 3,5.105 J
d) 0,9.103 J
e) 1,2.106 J
Gabarito: Letra a
Resolução:
Vamos usar a fórmula da energia potencial elétrica para resolver o exercício, observe:
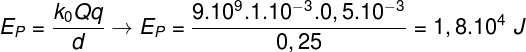
De acordo com o cálculo, a energia potencial elétrica desse sistema é igual a 1,8.10^4 J. Portanto, a alternativa correta é a letra a.
Artigos Relacionados

Últimas notícias
Outras matérias


















