Algarismos significativos

Os algarismos significativos são a quantidade de dígitos que um valor que representa medida ou cálculo envolvendo várias medidas contém. É costume confundirmos algarismos significativos com casas decimais, porém as casas decimais representam a quantidade de números contidos após a vírgula, e os algarismos significativos representam todos os dígitos, antes e depois da vírgula, havendo algumas ressalvas em relação à posição do zero.
Saiba mais: Números decimais — os números que possuem a vírgula como representante de uma parte não inteira
Resumo sobre algarismos significativos
-
Os algarismos significativos representam os valores das grandezas medidas ou calculadas.
-
Os algarismos duvidosos são as incertezas de um algarismo significativo. Trata-se dos últimos dígitos dos algarismos significativos, que representam a menor medida possível do equipamento utilizado.
-
Quando os zeros estão à esquerda, eles não contam como algarismos significativos.
-
Os zeros que estiverem à direita e entre outros números contam como algarismos significativos.
-
Quando o número estiver na forma de notação científica, os algarismos significativos são aqueles multiplicados pela potência de base 10.
-
Nas operações com algarismos significativos, o resultado sempre terá a mesma quantidade de dígitos daquele que possuir menos dígitos.
Quais são os algarismos significativos?
Os algarismos significativos são os dígitos que compõem os valores de alguma medida ou cálculo. Por exemplo, se for utilizada uma régua escolar comum de 30 centímetros para medir o comprimento de um lápis e for obtido o valor de 25,3 cm, essa medida possui três dígitos, logo possui três algarismos significativos.
É necessário observar que os valores decimais também fazem parte dos algarismos significativos. Caso fosse medida apenas a ponta do lápis após ser apontado e fosse obtido 1,0 centímetro, a medida teria dois algarismos significativos, pois apresenta dois dígitos.
O que são os algarismos duvidosos?
Quase todas as medidas não são exatas ou costumam ter seus valores arredondados. Levando isso em consideração, surgiu o conceito dos algarismos duvidosos, nomeados também como incertezas ou erro da medida. Eles são o último dígito do algarismo significativo.
Isso se dá porque geralmente a última casa da medida ou cálculo pode apresentar um determinado grau de imprecisão. As incertezas vêm antecedidas pelos sinais ± ou entre parênteses após o algarismo significativo.
Vamos considerar a régua escolar de 30 centímetros, o lápis e sua ponta mencionados anteriormente. O comprimento do lápis é de 25,3 cm, ou seja, 25 centímetros e 3 milímetros. Os milímetros representam a menor medida da régua, sendo assim, a imprecisão se encontra neles.
Levando em conta o erro da medida, o comprimento do lápis pode ser reescrito como 25,3±0,1 ou 25,3(0,1). Isso implica que a medida do lápis não poderá ser inferior a 25,2 cm ou superior a 25,4 cm, já que o erro é de 0,1 para mais ou para menos.
Quais são as regras que envolvem os algarismos significativos?
Os algarismos significativos englobam todos os números, porém quando se trata do 0, deve-se considerar os 3 casos a seguir.
-
Primeiro caso
Quando há apenas zeros do lado esquerdo de um número, eles não contarão como algarismos significativos.
Exemplo:
0,00254 → Há apenas 3 algarismos significativos, já que à esquerda do dígito 2 há apenas zeros.
-
Segundo caso
Se o 0 estiver à direita ou entre outros números, ele será considerado dígito do algarismo significativo.
Exemplo 1:
52,00 → Há 4 algarismos significativos, porque os zeros estão posicionados à direita. Isso se dá pois se os zeros são colocados ali, infere-se que aqueles dígitos são relevantes e poderiam assumir outro valor, devido ao algarismo duvidoso, o que é justamente o oposto de quando o zero está à esquerda, ocupando lugar fixo no algarismo.
Exemplo 2:
9,04 → Quando o 0 estiver entre números, ele constará como algarismo significativo. Sendo assim, esse número apresenta 3 algarismos significativos.
-
Terceiro caso
Quando o número estiver na forma de notação científica, os algarismos significativos serão aqueles multiplicados pela potência de base 10.
Exemplo:
3,26 · 106 → Esse número possui três algarismos significativos, já que o 3,26 que está sendo multiplicado pelo 106 possui três dígitos. Lembrando que 6 seria o algarismo duvidoso ou incerteza.
Como fazer arredondamento de algarismos significativos?
Em algumas situações, é necessário reduzir um número que é considerado muito extenso visualmente. Nesses casos, utiliza-se o arredondamento. Veja as situações a seguir.
-
Situação 1
Se o número posterior àquele que se deseja finalizar for igual ou maior que 5, deve-se adicionar 1 a esse número.
Exemplo:
0,458987 = 0,46 — O número após 5 é 8. Logo, acrescentando 1 a 5, obtemos 0,46.
-
Situação 2
Se o número posterior àquele que se deseja finalizar for menor que 5, deve-se manter esse número.
Exemplo:
0,005462331 = 0,005 — O número após 5 é 4. Sendo assim, mantém-se o 5.
Saiba também: Valor de pi — o número com trilhões de casas decimais que precisou ser arredondado
Quais operações podem ser feitas com algarismos significativos?
As operações envolvendo algarismos significativos seguem algumas regras. Veja a seguir.
-
Soma e subtração de algarismos significativos
Nas operações de soma ou subtração, o resultado deve sempre conter a quantidade de dígitos significativos do número que possui a menor quantidade de dígitos. Isso se dá por causa da incerteza, pois ela se encontra no último digito. Sendo assim, em um valor com menos dígitos, a incerteza aparecerá antes de um número com mais dígitos. Para isso, após a soma, o valor deve ser arredondado para ter a mesma quantidade de dígitos que aquele que possui menos algarismos.
Exemplo:
0,257 + 0,56 = 0,817 = 0,82 — O número 0,56 possui menos dígitos. Sendo assim, o resultado também deve ter dois dígitos.
-
Multiplicação e divisão de algarismos significativos
Na multiplicação ou divisão de algarismos significativos, o resultado deve seguir a mesma ideia da soma e da subtração. Realiza-se a operação e, após sua conclusão, arredonda-se o resultado para ele ter a mesma quantidade de algarismos significativos daquele que possui menos dígitos.
Exemplo 1:
0,24 · 75,2 = 18,048 = 18 — O algarismo significativo com menos dígitos é 0,24, que possui dois dígitos por apresentar um zero isolado à esquerda.
Exemplo 2:
2628908 ÷ 346 = 7598 = 760 — O resultado terá 3 algarismos significativos, já que 346 possui menos dígitos. Como após 9 no resultado vem 8, acrescenta-se 1 a 9, fazendo com que o resultado seja 760.
Exercícios resolvidos sobre algarismos significativos
Questão 1
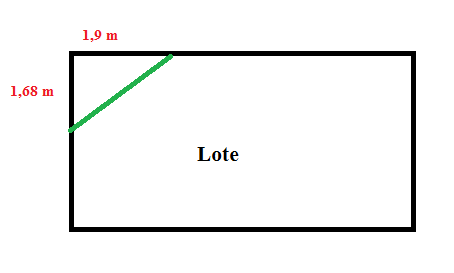
Liriosvaldo deseja construir uma pequena despensa de formato triangular na quina do seu lote. Para isso, ele mediu 1,68 m a partir do canto de um lado e 1,9 m a partir do outro, como demonstrado na figura a seguir. Marque a alternativa que representa o valor aproximado de cerâmica que ele deve comprar para assentar o piso da despensa.
A) 1,59 m²
B) 1 m²
C) 1,6 m²
D) 1,5 m²
E) 1,596 m²
Resolução:
Alternativa C
Para assentar cerâmica, é necessário conhecer a área. Logo, como a despensa forma um triângulo retângulo, a área será dada por:
\(A=\frac{b\bullet h}{2}\)
Considera-se a base b como a horizontal e a altura h como a vertical:
b = 1,9 m
h = 1,68 m
A = ?
\(A=\frac{1,9\bullet1,68}{2}=\frac{3,192}{2}=1,596\)
\(A=1,6{\ m}^2\)
O resultado apresentou dois dígitos porque o 1,9 é o algarismo significativo com menos casas. Como o 2 faz parte da fórmula da área do triângulo, ele não é utilizado para determinar o número de dígitos da resposta.
Questão 2
Um ônibus de turismo, ao fazer rota por uma cidade com diversos pontos turísticos, partiu da posição 1,54 km na cidade e foi até a posição 166,6 km em aproximadamente 5,46 horas. Considerando a norma dos algarismos significativos, qual é a velocidade média do ônibus ao realizar esse passeio?
A) 30,2 km/h
B) 30,23 km
C) 30 km/h
D) 3 km/h
E) 31 km/h
Resolução:
Alternativa A
Extraindo os dados:
t = 5,46 horas
si = 1,54 km
sf = 166,6 km
vm = ?
A fórmula de velocidade média é dada por
\(v_m=\frac{s_f-s_i}{t}=\frac{166,6-1,54}{5,46}=\frac{165,06}{5,46}=30,23077\ km/h\)
\(v_m=30,2\ km/h\)
Como o algarismo significativo com menos dígitos é 5,46, a resposta também terá 3 casas.
Artigos Relacionados

Últimas notícias
Outras matérias


















