Fórmula de Taylor

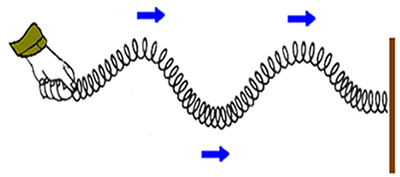
A figura abaixo mostra-nos a criação de uma onda transversal periódica. Damos o nome de ondas periódicas àquelas que são produzidas por fontes que executam oscilações periódicas, ou seja, são ondas que se repetem em intervalos regulares de tempo.
De acordo com a figura acima, em uma onda formada por uma corda, podemos identificar as cristas, que são os pontos mais altos dos pulsos; os vales, que são os pontos mais baixos do pulso de onda; a amplitude, que corresponde ao maior afastamento que cada ponto em comum da onda apresenta (por exemplo, a distância entre uma crista e um vale); o período, que é o intervalo de tempo para que cada ponto homogêneo da onda execute uma oscilação; a frequência, que é o número de oscilações completas que cada ponto homogêneo da onda executa; e, por fim, o comprimento de onda, que representa a distância entre duas cristas ou dois vales.
A propagação de uma onda periódica em um meio homogêneo e isotrópico é caracterizado como movimento uniforme. Sendo v a velocidade de propagação de uma onda, podemos escrever o seguinte:
![]()
Se observarmos bem uma onda periódica, veremos que em um determinado período, ou seja, em um determinado intervalo de tempo, a onda consegue deslocar-se por um comprimento de onda. Sendo assim, na equação acima, ∆s= λ e ∆t= T, mas, como o período é o inverso da frequência, temos que IMAGEM DO TEXTO. Dessa forma, podemos escrever:
v=λ .f
Devemos ficar atentos ao fato de a frequência de uma onda sempre ser a mesma frequência da fonte produtora da onda. Dessa forma, independentemente do meio em que a onda propaga-se, sua frequência não será modificada. Devemos lembrar também que a velocidade de propagação de uma onda mecânica em um determinado meio só depende das propriedades elásticas do meio.
Fórmula de Taylor
As cordas tensionadas, ou seja, cordas esticadas, constituem ótimos meios para observar a propagação de ondas transversais. Considerando uma corda homogênea e de secção constante, de massa m e comprimento L, sua densidade linear de massa (ρ) é:
![]()
Podemos ver que, em relação à propagação de um pulso transversal ou de uma onda periódica transversal na corda, a velocidade com que uma onda periódica propaga-se depende da densidade linear (ρ) da corda e da intensidade da força tensora (F) a que ela está sujeita.
Esse estudo, feito experimentalmente por Marin Mersenne, com cordas vibrando com baixa frequência e cordas de instrumentos sonoros, foi utilizado matematicamente pelo britânico Brook Taylor.
Assim, podemos determinar a velocidade de propagação de uma onda usando a equação que ficou conhecida como Fórmula de Taylor, descrita a seguir:
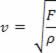
Na equação acima, v é a velocidade de propagação, F é a intensidade da força de tração exercida na corda e ρ é a densidade linear da corda.
Artigos Relacionados

Últimas notícias
Outras matérias