Medida do coeficiente de atrito estático
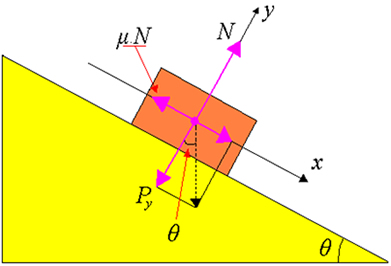
São inúmeras as situações em que observamos o movimento de objetos deslizando sobre planos inclinados. Um plano inclinado é uma superfície inclinada em relação à horizontal, sobre as quais os objetos podem deslizar pela ação da força da gravidade. Exemplos: escorregadores, ladeiras, tobogãs e caçambas de caminhão descarregando.
Em algumas situações, relacionadas ao estudo do plano inclinado, veremos a adoção de um plano sem atrito; já em outras situações consideraremos o atrito. Para um plano inclinado, no qual se leva em consideração o atrito, temos a possibilidade de determinar o valor do coeficiente de atrito entre o corpo e a superfície de contato.
Vejamos então a figura acima: se colocarmos um corpo sobre um plano inclinado com atrito e lentamente formos aumentando a inclinação do plano, veremos que o corpo começará a deslizar a partir de um certo ângulo. Esse ângulo é denominado ângulo limite ou ângulo máximo. Aqui representaremos o ângulo limite por θm. Portanto, podemos concluir que esse é o ângulo máximo que o plano inclinado pode ter sem que o objeto escorregue (veja a figura acima).
Nesse ponto, a força de atrito vale μe.N. Colocando ax=0 e o valor de θm na expressão para ax calculada acima, obtemos:
g.senθm-μe.g.cosθm=0
Isolando o coeficiente de atrito μe, obtemos:
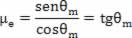
Vejamos um exemplo:
Um certo tobogã, sem a lubrificação da água, apresenta um coeficiente de atrito μ = 0,3. Determine qual será a aceleração experimentada pela boia no segmento de 45º.
Resolução:
Como sabemos, o tobogã é um plano inclinado com atrito, sendo assim há a necessidade de incluir a força de atrito no esquema da resolução. O esquema é o seguinte:
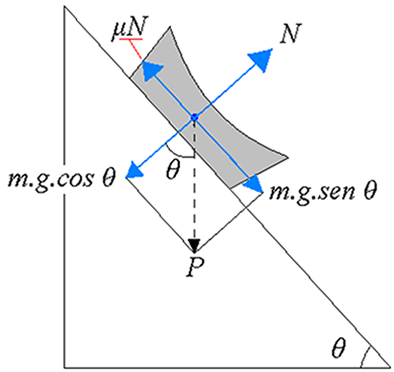
De acordo com a segunda Lei de Newton para as componentes y:
Ftotal y=m.ay
N-m.g.cos θ=m.ay=0
N=m.g.cos θ
Encontrando o valor da força normal
As componentes sobre o eixo x resultam em:
Ftotal x=m.ax
m.g.sen θ-μ.N=m.ax
m.g.sen θ-μ.m.g.cosθ=m.ax
Isolando a aceleração ax, obtemos:
ax=g.sen θ-μ.g.cosθ
Para uma inclinação de 45º, temos:
sin45°≅0,71
cos45°≅0,71
e usando o coeficiente de atrito dado no enunciado μ = 0,3 e g = 10 m/s2, calculamos o valor numérico de ax:
ax=10 x 0,71-0,3 x 10 x 0,71
ax=4,97 m/s2
Portanto, a aceleração do tobogã seco é de 4,97 m/s2.
Artigos Relacionados

Últimas notícias
Outras matérias


















