Multiplicando um vetor por um número

Nos nossos estudos sobre grandezas vetoriais, fazemos uso de uma seta cuja direção sempre aponta para a direita. Essa seta recebe o nome de vetor e por definição é um ente matemático que representa o conjunto dos segmentos orientados de reta que possui um módulo, uma direção e um sentido. Em diversas situações podemos utilizar vetores, tanto em soma, subtração ou multiplicação. Na multiplicação de dois vetores devemos fazer o produto do vetor pelo seu valor numérico. Abaixo temos a definição da multiplicação vetorial.
Vamos imaginar um número real cujo valor seja k, sendo k ≠ 0 e um vetor 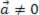 . O produto de k por
. O produto de k por .jpg) é um vetor
é um vetor 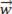 , representado por:
, representado por:
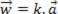
Cujas características são:
Característica 1
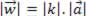
Característica 2
A direção de 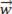 é a mesma de
é a mesma de .jpg) .
.
Característica 3
Se k > 0, 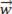 e
e .jpg) possuem o mesmo sentido;
possuem o mesmo sentido;
Se k < 0, 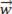 e
e .jpg) possuem sentidos opostos;
possuem sentidos opostos;
Se k = 0 ou 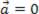 , o produto é o vetor nulo.
, o produto é o vetor nulo.
Sendo k ≠ 0, o produto 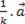 pode ser indicado por
pode ser indicado por  .
.
Por exemplo, na figura abaixo temos um vetor .jpg) com |
com |.jpg) | = U. O vetor 2
| = U. O vetor 2.jpg) tem módulo 2 e o mesmo sentido de
tem módulo 2 e o mesmo sentido de .jpg) . O vetor _3
. O vetor _3.jpg) possui módulo 3 e sentido oposto ao de
possui módulo 3 e sentido oposto ao de .jpg) .
.
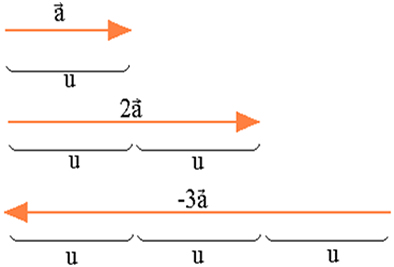
Na figura acima temos:
|2.jpg) | = |2| . |
| = |2| . |.jpg) | = 2u
| = 2u
|_3.jpg) | = |_3| . |
| = |_3| . |.jpg) | = 3u
| = 3u
Na figura abaixo, o vetor .jpg) possui módulo 4. O vetor
possui módulo 4. O vetor  possui módulo 2.
possui módulo 2.
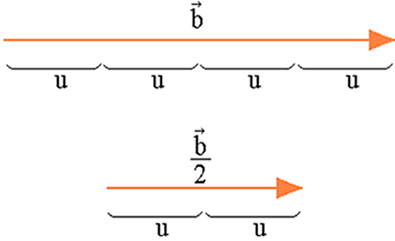
Na figura acima temos como resultado:
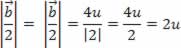
Artigos Relacionados

Últimas notícias
Outras matérias


















