Ondas estacionárias
Ondas estacionárias são oscilações periódicas produzidas pela interferência entre ondas de frequência igual e que se propagam ao longo da mesma direção, mas em sentidos opostos. Quando uma onda incidente encontra-se com uma onda refletida por uma extremidade fixa de uma corda, formam-se ondas estacionárias, também conhecidas como harmônicos. As ondas estacionárias são assim chamadas pelo fato de não se propagarem ao longo do espaço. Suas oscilações ocorrem exclusivamente na direção perpendicular (90º) à direção das ondas que as produziram.
Veja também: Ressonância – o curioso fenômeno que dá origem às notas musicais
Características das ondas estacionárias
As ondas estacionárias, também chamadas de harmônicos, resultam de uma superposição entre diferentes ondas. O fenômeno que dá origem a elas é a ressonância. É por esse motivo que essas ondas são usadas para a produção das notas tocadas nos instrumentos musicais de corda e de sopro, por exemplo.

Quando uma onda estacionária é formada, alguns pontos do espaço permanecem em repouso durante todo o tempo. Esses pontos são chamados de nós. Os nós são, portanto, regiões de interferência destrutiva total. Em uma corda vibrante, por exemplo, a formação de uma onda estacionária sempre dá origem a pelo menos dois nós, encontrados nas extremidades onde a corda encontra-se fixada.
Além dos nós, as ondas estacionárias também apresentam antinós. Esses pontos, também chamados de crista e vale, diferentemente dos nós, são pontos de interferência construtiva entre as duas ondas e estão sempre em movimento.
Chamamos de comprimento de onda a distância entre três nós consecutivos ou ainda a distância entre dois antinós consecutivos. O comprimento de onda é também o tamanho ocupado por uma oscilação completa. Além disso, a medida do comprimento de onda é limitada ao espaço disponível para a formação de ondas estacionárias, como o comprimento da corda em que essas ondas se formaram.
Veja também: Classificação das ondas – natureza, propagação e vibração
Ondas estacionárias em cordas
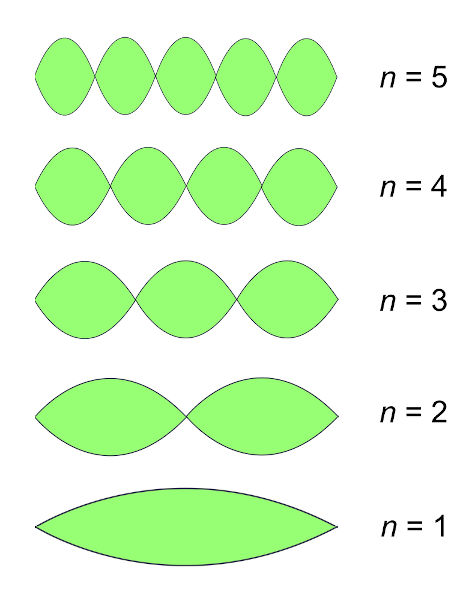
Ondas estacionárias em cordas são formadas quando uma oscilação incide sobre a extremidade fixa de uma corda. Quando isso acontece, essa onda é refletida com uma inversão de fase, isto é, a amplitude da onda tem sua direção de oscilação e propagação invertida. De acordo com a frequência da onda, o comprimento de onda das ondas estacionárias muda – quanto maior é sua frequência, menor é o comprimento de onda. Além disso, para que se formem ondas estacionárias em cordas, é necessário que o comprimento da corda seja um múltiplo inteiro (n = 1,2,3,4 ….) da metade do comprimento de onda, denotado pelo símbolo λ.
A fórmula que relaciona o comprimento da corda (L) com o comprimento de onda (λ) é mostrada a seguir:
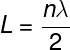
n – ordem do harmônico
Na fórmula acima, o número inteiro n é conhecido como ordem do harmônico. De acordo com o tamanho da corda, para uma determinada frequência, existe um número finito de harmônicos que podem ser formados. Entre todos eles, o harmônico de menor frequência é o harmônico cujo n = 1, conhecido como harmônico fundamental.
Ondas estacionárias em tubos sonoros
Ondas estacionárias também são formadas quando o ar flui através de tubos sonoros. Quando isso acontece, é possível produzir sons mais intensos. Existem dois tipos de tubos sonoros: tubos abertos e tubos fechados. A seguir, vamos aprender como é possível calcular o comprimento de onda e a frequência das ondas sonoras nesses tipos de tubos.
→ Comprimento de onda e frequência em tubos abertos
Tubos abertos são aqueles que têm suas duas extremidades abertas. Nesses tubos só são produzidas ondas estacionárias cujos antinós (crista e vale) formam-se nas aberturas do tubo, e os nós, ao longo de seu interior.
As fórmulas usadas para calcular o comprimento de onda e a frequência da enésima onda estacionária (harmônico de ordem n) formada em um tubo aberto de comprimento L são mostradas a seguir:
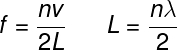
→ Comprimento de onda e frequência em tubos fechados
Os tubos sonoros fechados são aqueles que apresentam uma de suas extremidades fechada. Quando uma onda estacionária é estabelecida em um tubo desse tipo, nós são formados ao longo do tubo, bem como sobre sua extremidade tampada. Já na extremidade aberta, formam-se uma crista e um vale.
A ordem dos harmônicos nos tubos fechados é determinada por um múltiplo inteiro e ímpar (n = 1, 3, 5, 7) de um quarto do comprimento de onda (λ/4). As fórmulas usadas para calcular o comprimento de onda e a frequência de uma onda estacionária formada em um tubo sonoro fechado de comprimento L são mostradas a seguir:
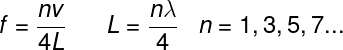
Veja também: Ondas eletromagnéticas – rádio, micro-ondas, ultravioleta e raios x
Exercícios resolvidos sobre ondas estacionárias
Questão 1 — Com relação às principais características das ondas estacionárias, assinale a alternativa correta.
a) Só podem ser produzidas por ondas de propagação transversal.
b) Só podem ser produzidas por ondas de propagação longitudinal.
c) São caracterizadas por se propagar pelo espaço com velocidade crescente.
d) São formadas pela interferência entre duas ondas de frequências iguais, que se movem em sentidos opostos.
e) São ondas de natureza mecânica, formadas exclusivamente em cordas ou em tubos sonoros.
Resolução: letra D.
Questão 2 — Uma corda de 20 cm de comprimento é colocada para oscilar, passando a ser percorrida por ondas estacionárias de comprimento de onda igual a 5 cm. A ordem do harmônico dessa onda é:
a) 2
b) 4
c) 8
d) 3
e) 5
Resolução:
Para calcular a ordem do harmônico, devemos usar a fórmula que relaciona o comprimento da corda com o comprimento de onda.
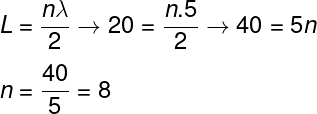
Artigos Relacionados

Últimas notícias
Outras matérias


















