O que é o plano inclinado?

Q: O que é o plano inclinado?

Plano inclinado é qualquer superfície que faça um ângulo, diferente de zero, com o horizonte, formando uma figura geométrica triangular. Alguns exemplos de planos inclinados são rampas, esteiras rolantes, escadarias e tudo que esteja inclinado.

Plano inclinado

Plano inclinado é a parte da Dinâmica que trabalha com o movimento em superfícies que formam um ângulo com o eixo horizontal.

Representação das diferentes inclinações de um plano dependendo do ângulo que ele faz com o eixo horizontal.

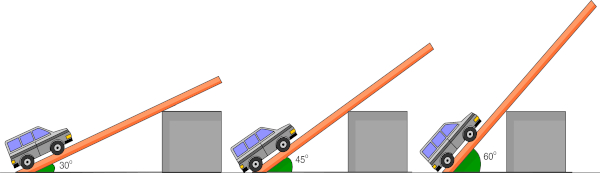
Plano inclinado é a parte da Dinâmica newtoniana que estuda o movimento dos objetos inclinados em superfícies que formam um ângulo com o eixo horizontal, com ou sem atrito. Podemos encontrá-lo em rampas, escadarias, facas, ou seja, tudo que gere um movimento inclinado.

Para calculá-lo, utilizamos a segunda lei de Newton, que determina que a força resultante que atua no bloco é igual ao produto da massa pela aceleração. Também utilizamos a fórmula da força peso. Caso haja atrito atuando sobre o bloco, usamos a fórmula da força de atrito.

Resumo sobre plano inclinado

Plano inclinado é o termo usado para designar situações da Física Dinâmica em que ocorrem movimentos em planos com inclinações.
Existem dois casos de exercícios com plano inclinado: quando há ou quando não há a força de atrito atuando sobre o objeto em movimento.
Para calcular o plano inclinado, a fórmula mais utilizada é a segunda lei de Newton, que determina que a força resultante é a massa multiplicada pela aceleração.
A força resultante é a soma ou a subtração das forças atuantes no corpo. Para descobrir seu valor, usamos várias fórmulas, tais como a da força peso ou da força de atrito.

Videoaula sobre plano inclinado

Não pare agora... Tem mais depois da publicidade ;)

O que é plano inclinado?

Plano inclinado é qualquer superfície que faça um ângulo, diferente de zero, com o horizonte, formando uma figura geométrica triangular. Alguns exemplos de planos inclinados são rampas, esteiras rolantes, escadarias e tudo que esteja inclinado.

Tipos de plano inclinado

São dois os casos em que trabalhamos com o plano inclinado: quando o objeto não está atritando com a superfície e quando ele está. Sabemos de qual caso se trata de acordo com as informações do enunciado.

Plano inclinado sem atrito

No caso do plano inclinado sem a força de atrito $\vec{f_{at}}$, as forças presentes no bloco sempre são a força normal $\vec{N}$, que é perpendicular à superfície do plano, e a força peso $\vec{P}$, que aponta para o centro da Terra (na maioria dos casos, para baixo). Caso haja algo puxando o bloco, haverá também a força que puxa $\vec{F}$. Na imagem, podemos ver as forças atuantes no plano contido no plano inclinado sem atrito.

Representação de forças que atuam sobre plano inclinado sem atrito

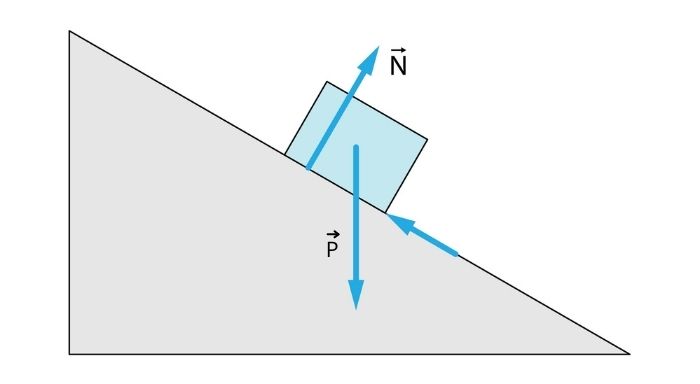
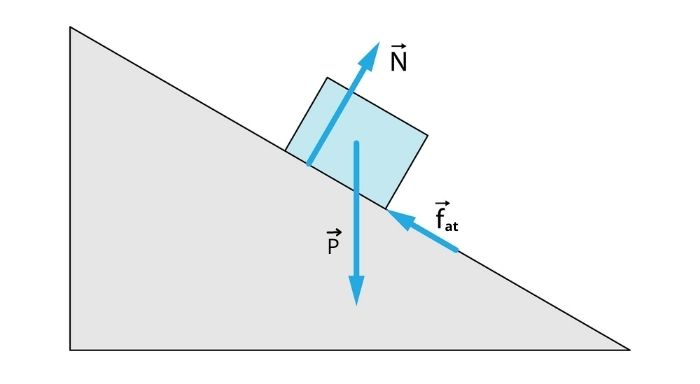
Plano inclinado com atrito

No caso do plano inclinado com a força de atrito $\vec{f_{at}}$, essa força atua rente ao chão seguindo o movimento, como se estivesse arrastando o chão, conforme a imagem abaixo:

Representação de forças que atuam sobre caixa no chão

Além disso, há a força normal $\vec{N}$, a força peso $\vec{P}$ e caso haja algo puxando o bloco, haverá também a força que puxa $\vec{F}$. Na imagem, podemos ver as forças atuantes no plano contido no plano inclinado com atrito.

Representação de forças que atuam sobre plano inclinado com atrito.

Decomposição das forças em exercícios de plano inclinado

Em exercícios de plano inclinado, é comum que usemos um artifício matemático chamado de decomposição da força, que nada mais é que “quebrar” o vetor em duas direções: na vertical, que é a coordenada $y$, e na horizontal, que é a coordenada $x$. Ou seja, a força $\vec{P}$ virará $\vec{P_x}$ e $\vec{P_y}$ , conforme a imagem abaixo:

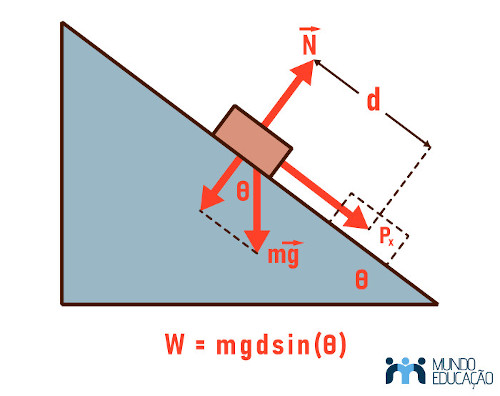
Decomposição de forças atuantes em bloco sobre plano inclinado

Força resultante no plano inclinado

A segunda lei de Newton é utilizada para calcular a força resultante em um bloco, que é a soma ou subtração das forças atuantes em uma mesma direção no bloco.

A soma (forças em um mesmo sentido) ou subtração (forças em sentidos opostos) das forças será determinada pelo modelo do exercício. Por exemplo, podem haver casos em que a força peso se some à força de atrito, enquanto em outros elas podem se subtrair.

Vale ressaltar que sentido diz respeito a direita e esquerda, e direção diz respeito a vertical, horizontal ou diagonal.

Fórmulas de plano inclinado

As fórmulas utilizadas nos exercícios de plano inclinado são a segunda lei de Newton (Princípio Fundamental da Dinâmica), que determina que a força resultante é calculada usando as fórmulas da força peso, a fórmula da decomposição da força peso e, em alguns casos, a força de atrito.

Segunda lei de Newton

$\vec{F_R}=m\bullet\vec{a}$

- $\vec{F_R}$ é a força resultante no bloco. Trata-se da soma (caso as forças estejam orientadas para o mesmo lado) ou subtração (caso as forças estejam em lados opostos) de todas as forças na horizontal ou na vertical. É medida em newton [N].
- $m$ é a massa do objeto, medida em quilogramas [kg].
- $\vec{a}$ é a aceleração do objeto, medida em metros por segundo ao quadrado $[m/s^2]$.
Força peso

$\vec{P}=\ m\bullet\vec{g}$

- $\vec{P}$ é a força peso, medida em newton [N].
- $m$ é a massa do objeto, medida em quilogramas [kg].
- $\vec{g}$ é a aceleração da gravidade, medida em metros por segundo ao quadrado $[m/s^2]$.
Decomposição da força peso

$\vec{P_x}=P\bullet sen\ \theta$

$\vec{P_y}=P\bullet cos\ \theta$

$\vec{P_x}$ é a coordenada horizontal da força peso, medida em newton [N].
$\vec{P_y}$ é a coordenada vertical da força peso, medida em newton [N].
$P\ $ é o módulo da força peso, medida em newton [N].
$sen\ \theta$ é o seno do ângulo de inclinação do plano, medido em graus.
$cos\ \theta$ é o cosseno do ângulo de inclinação do plano, medido em graus.

Força de atrito

$\vec{f_{at}}=\mu\bullet\vec{N}$

- $\vec{f_{at}}$ é a força de atrito, medida em newton [N].
- $\mu$ é o coeficiente de atrito. Ele pode ser estático, quando o bloco está na iminência do movimento (quase se movimentando), ou cinético, quando o bloco está se movimentando. Não possui unidade de medida.
- $\vec{N}$ é a força normal, medida em newton [N].

Observação: Caso não seja dada a aceleração do objeto, podemos calculá-la utilizando as fórmulas do MUV.

Exercícios resolvidos sobre plano inclinado

Questão 01

(Unimep-SP) Um bloco de massa 5kg é arrastado ao longo de um plano inclinado sem atrito, conforme a figura.

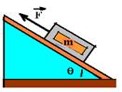
Bloco de 5kg em plano inclinado

Para que o bloco adquira uma aceleração de $3m/s^2$ para cima, a intensidade de $ \vec{F}$ deverá ser:

($g=10\ m/s²$, $sen\ \theta=0,8$ e $cos\ \theta=0,6$)

a) igual ao peso do bloco

b) menor que o peso do bloco

c) igual à reação do plano

d) igual a 55N

e) igual a 10N

Resolução

Alternativa D

Primeiramente, encontraremos as forças que estão atuando no bloco. Neste caso, há a força normal $\vec{N}$, que é perpendicular à superfície, mas não é relevante para o cálculo, há a força que puxa $\vec{F}$ e a força peso $\vec{P}$. Deve-se decompor a força peso em duas: $\vec{P_x}$ na horizontal e $\vec{P_y}$ na vertical, seguindo o plano cartesiano.

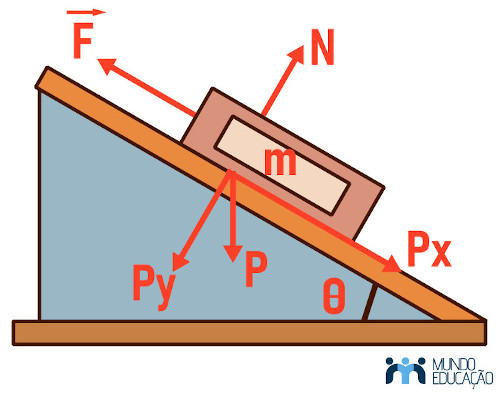
$\vec{P_y}$

Utilizando a segunda lei de Newton, que diz que a soma de todas as forças envolvidas é igual à massa multiplicada pela aceleração, obtemos a expressão:

$\vec{F}-\vec{P_x}=m\bullet\vec{a}$

Usando a fórmula de decomposição da força peso, temos $\vec{P_x}=P\bullet sen\ \theta$. Então:

$\vec{F}-P\bullet sen\ \theta=m\bullet\vec{a}$

$\vec{F}-m\bullet g\bullet sen\ \theta=m\bullet\vec{a}$

Substituindo os dados:

gravidade: 10 m/s²
aceleração: 3 m/s²
massa: 5 kg
sen $\theta=0,8$

$\vec{F}-5\bullet10\bullet0,8=5\bullet3$

$\vec{F}-40=15$

$\vec{F}=55\ N$

Questão 2

(Uerj — adaptado) Um bloco de massa igual a 1,0 kg repousa em equilíbrio sobre um plano inclinado. Esse plano tem comprimento igual a 50 cm e alcança uma altura máxima em relação ao solo igual a 30 cm. Calcule o coeficiente de atrito entre o bloco e o plano inclinado.

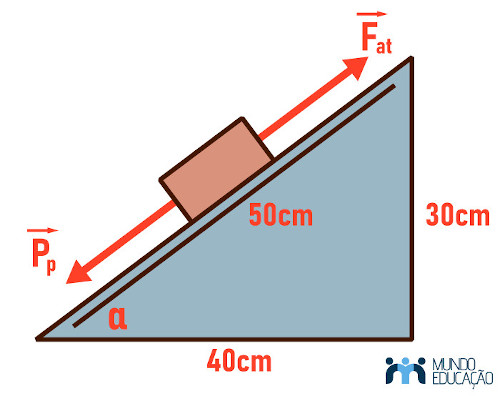
Bloco de 1,0 kg em plano inclinado com atrito

Resolução

O plano inclinado é formado por um triângulo retângulo de hipotenusa 50 cm e cateto 30 cm. Por meio do teorema de Pitágoras, determinamos o outro cateto, que deve ser de 40 cm. Assim, conseguimos encontrar o valor do seu seno e cosseno.

$sen\ \alpha=30/50=0,6$

$cos\ \alpha=40/50=0,8$

Como o bloco está em equilíbrio, a força resultante sobre ele é nula. Assim:

${\vec{P}}_P=\vec{f_{at}}$

Decompondo a força peso de forma similar ao exercício anterior e lembrando que a força normal é igual a $\vec{P_y}$, temos:

$\vec{P_x}=\mu\bullet\vec{N}$

$\vec{P_x}=\mu\bullet\vec{P_y}$

Usando a fórmula de decomposição da força peso, $\vec{P_y}=\vec{P}\bullet cos\ \alpha$, temos:

$P\bullet sen\ \alpha=\mu\bullet\vec{P}\bullet cos\ \alpha$

$m\bullet g\bullet sen\ \alpha=\mu\bullet m\bullet g\bullet cos\ \alpha$

Substituindo pelos valores dados no enunciado e usando a gravidade como $10\ m/s^2$, obtemos:

$1\bullet10\bullet0,6=\mu\bullet1\bullet10\bullet0,8$