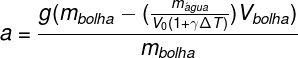Termômetro de Galileu

Uma das formas mais criativas e bonitas de se aferir a temperatura ambiente é por meio do Termômetro de Galileu, um aparato que recebe o nome do seu inventor, o físico italiano Galileu Galilei (Quer saber mais sobre esse grande cientista? Acesse este link). Esse bonito instrumento de medida também é conhecido como Termoscópio de Galileu, uma vez que suas medidas de temperatura não são as mais precisas, além de o dispositivo funcionar somente para pequenos intervalos de temperatura, que variam geralmente entre 18ºC e 28ºC.
Como ele foi construído?
Esse tipo de termômetro consiste em uma coluna de vidro preenchida com líquido (água, parafina líquida ou álcool). Em seu interior, são colocadas várias “bolhas” de vidro, preenchidas com algum tipo de líquido em diferentes colorações. Cada uma dessas pequenas bolhas leva uma etiqueta metálica correspondente a uma temperatura. Essa etiqueta atua como um contrapeso precisamente calibrado para que a densidade de cada uma dessas pequenas esferas seja aproximadamente igual.
Como funciona?
.jpg)
Quando a temperatura ambiente varia, a água no interior do tubo lentamente muda de temperatura até atingir o equilíbrio térmico. Essa variação de temperatura causa na água uma dilatação ou contração em seu volume. Como consequência da mudança de volume na água, sua densidade também muda, afetando o módulo da força de empuxo sobre cada uma das esferas, que possuem volumes ligeiramente diferentes.
A calibração do equipamento é feita para diferentes valores de temperatura ambiente, e a sua leitura correta é sempre feita pela bolha de vidro que estiver na parte mais baixa do tubo. Sobre cada uma das pequenas bolhas de vidro haverá uma força resultante, dada pela diferença da força peso com a força de empuxo. O módulo dessa força resultante pode ser calculado por meio da 2ª Lei de Newton:
-
P: é o peso de cada bolha de vidro;
-
E: é o empuxo sofrido por ela;
-
m: é a sua massa;
-
a: é o módulo da aceleração adquirida por ela.
Não pare agora... Tem mais depois da publicidade ;)
De acordo com o Teorema do Empuxo, descrito por Arquimedes, quando um corpo ocupa o espaço de um fluido, ele sofre a ação de uma força vertical e para cima proporcional ao volume de fluido deslocado, à densidade e à gravidade local, de forma que podemos expressar a aceleração adquirida por cada uma das bolhas por:
No caso em que a aceleração for positiva, o peso das bolhas de vidro será maior que o empuxo do líquido, portanto, elas afundarão; no caso contrário, flutuarão. A única grandeza variável na equação acima é a densidade (d) do líquido em razão da dilatação (ou contração) térmica. A dilatação volumétrica sofrida pela água pode ser calculada de forma bastante simples. Veja a fórmula:
Na equação acima, V é o volume final da água, V0 é o seu volume final, γ é o coeficiente de dilatação volumétrica, e ΔT é a variação de temperatura ambiente. Como a densidade do líquido é determinada pela razão de sua massa por seu volume, temos que:
A densidade da água em função da variação da temperatura ambiente pode ser escrita como:
Incorporando todas as equações acima à aceleração, podemos perceber que a aceleração sofrida pelas bolhas de vidro é uma função da variação de temperatura.
A ideia utilizada por Galileu, extremamente engenhosa, é uma forma válida de se medir temperaturas, porém, é necessário que se espere um tempo até que toda a água atinja o equilíbrio térmico e cessem as correntes de convecção a fim de se obter a medida de temperatura mais acurada possível.
OBS.: Desconsideramos aqui os efeitos de turbulência da água, bem como a força resistiva de atrito em seu interior. Levando em conta esses efeitos, teríamos resultados mais precisos, porém, de execução muito mais complexa.
Artigos Relacionados

Últimas notícias
Outras matérias