A Lei dos Senos - compreendendo sua aplicação
A utilização da definição do seno de um ângulo nos acompanha desde o início do estudo das relações trigonométricas de um triângulo, entretanto a utilização da relação do valor do seno com o cateto e hipotenusa, só deve ser aplicada em triângulos retângulos, contudo, sabemos que existem inúmeros casos que não teremos somente triângulos retângulos.
Para isso temos a Lei dos senos, que relaciona os lados do triângulo e os senos de seus ângulos em uma relação de proporcionalidade, possibilitando assim, utilizarmos o valor numérico dos senos em todos os triângulos.
Antes de analisarmos a aplicação desta lei, vamos recordar qual é esta relação de proporcionalidade. (Vale ressaltar que a demonstração desta lei pode ser encontrada no tópico Lei dos senos.
.jpg)
Para que seja possível a aplicação desta lei, precisaremos apenas do valor dos ângulos e o valor de apenas um dos lados, com estes dados, poderemos encontrar o valor dos outros dois lados, apenas aplicando a lei dos senos.
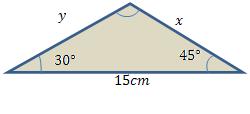
Veja um exemplo, para termos certeza de que isto é possível.
Façamos a nossa relação de proporcionalidade:
![]()
Veja que as medidas x e y podem ser expressas pelas seguintes igualdades.
![]()
Observe que nas duas igualdades utilizamos apenas os valores dos senos dos ângulos e a medida dos lados que conhecemos. Com isso, podemos concluir que para encontrarmos todas as medidas de um triângulo, basta conhecermos seus ângulos e um de seus lados.
Curiosidade: Aplique a lei dos senos em um triângulo retângulo e observe a expressão obtida!