Aplicação da relação entre volumes
Uma prática comum na matemática é a de relacionar elementos de objetos diferentes, buscando encontrar termos que sejam equivalentes, a partir de algumas condições impostas.
No artigo Relação entre volumes podemos ver um estudo mais generalizado, que busca comparar medidas entre um cubo e um cilindro e entre cilindros de medidas diferentes.
Tendo essa comparação em vista, estudaremos casos em que se faz necessária uma análise das expressões algébricas (fórmulas) que determinam o volume de cada sólido.
No último ENEM (Exame Nacional do Ensino Médio) tivemos dois casos nos quais era necessário estudar o volume de dois sólidos ao mesmo tempo, de modo que os volumes desses sólidos tivessem uma relação entre si.
Vejamos um desses problemas:
Questão 164 (ENEM – 2010)
"Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.
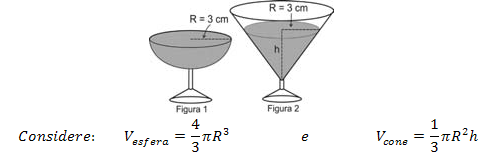
Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de;"
Note que os noivos solicitaram que o volume entre as duas taças seja o mesmo, portanto devemos explicitar a relação entre o volume das taças, de modo a conseguir determinar o valor da altura que fará com que o volume da taça em formato de hemisfério seja igual ao da taça de formato de cone.
Foi-nos informada a expressão dos volumes da esfera e do cone, entretanto, a taça não é uma esfera completa e sim “metade” de uma esfera, portanto devemos determinar uma expressão para o volume da Figura 1.
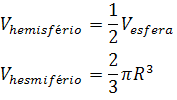
Devemos ter o volume do hemisfério igual ao volume da figura 2, portanto:
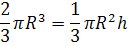
Após substituirmos os dados que o exercício nos deu, veremos que só nos falta o valor da altura, que é justamente a medida que determinará a relação de igualdade entre as duas taças.
.png)
Como podemos notar, ao buscar relações entre dois volumes, encontramos condições sobre as medidas que determinam esses volumes de forma que exista de fato uma relação de igualdade entre eles. Para obtermos essas condições, basta relacionarmos de forma correta as expressões dos volumes e os cálculos algébricos.
Por Gabriel Alessandro de Olivera
Graduado em Matemática
Artigos Relacionados

Últimas notícias
Outras matérias


















