Círculo e circunferência

Círculo e circunferência são duas figuras geométricas muito parecidas, o que pode ocasionar dúvidas sobre as suas definições. Vamos à diferenciação:
-
Definição de circunferência
Uma circunferência é um conjunto de pontos pertencentes ao plano que, dado um ponto fixo C, possuem a mesma distância até o ponto C. Em outras palavras, dada a distância “r” e o ponto fixo C, qualquer ponto A que possui a distância de A até C igual a r é um ponto pertencente à circunferência. Matematicamente, podemos representar essa última relação da seguinte maneira:
dAC = r
Tendo em vista a distância entre dois pontos obtida na Geometria Analítica e considerando as coordenadas de A (x,y) e de C (a,b), a relação acima pode ser reescrita da seguinte maneira:
dAC = r
√[(a – x)2 + (b – y)2] = r
(a – x)2 + (b – y)2 = r2
Na Geometria Analítica, essa equação é chamada de equação da circunferência com centro C (a,b) e raio r.
O ponto C é conhecido como centro da circunferência e a distância r é chamada de raio. A figura geométrica formada por um conjunto de pontos desse tipo é a seguinte:
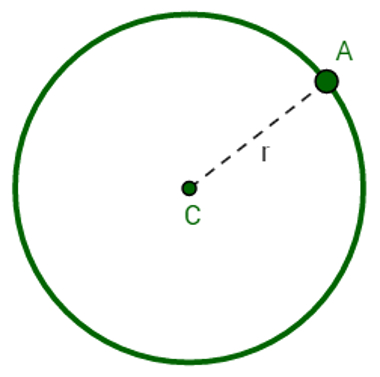
Circunferência de centro C e raio r
O ponto C não pertence à circunferência, pois a circunferência é apenas o círculo verde. O ponto A, por sua vez, pertence à circunferência.
-
Definição de círculo
O círculo, por sua vez, é uma figura geométrica plana que é definida da seguinte maneira:
Círculo é o conjunto de pontos resultantes da união entre uma circunferência e seus pontos internos. Em outras palavras, o círculo é a área cuja fronteira é uma circunferência.

Círculo: área colorida
Tomando novamente os conhecimentos vindos da Geometria Analítica, a equação do círculo é praticamente igual à equação da circunferência. A diferença encontra-se no fato de o círculo ser um conjunto de pontos menor ou igual ao raio. A partir disso, temos a seguinte equação:
dAC ≤ r
√[(a – x)2 + (b – y)2] ≤ r
(a – x)2 + (b – y)2 ≤ r2
Dessa maneira, a diferença fundamental entre círculo e circunferência é que o círculo é toda a área interna de uma circunferência. Já essa última é apenas o contorno de um círculo.
Propriedades básicas do círculo e da circunferência
O ponto C, centro da circunferência, não pertence a ela, mas pertence ao círculo. Dessa maneira, dado um ponto A qualquer (lembrando que dAC é a distância entre A e C), as posições relativas entre A e uma circunferência são:
1 – A é ponto da circunferência, se dAC = r;
2 – A é ponto externo à circunferência, se dAC > r;
3 – A é ponto interno à circunferência, se dAC < r;
As posições relativas entre A e o círculo são:
1 – A é ponto do círculo, se dAC ≤ r
2 – A é ponto externo ao círculo, se dAC > r
Qualquer segmento que liga dois pontos pertencentes a uma circunferência é chamado de corda. Quando uma corda contém o centro da circunferência, ela também é chamada de diâmetro. Desse modo, o diâmetro tem o comprimento igual ao comprimento de dois raios e, além disso, é a maior corda encontrada em qualquer circunferência.
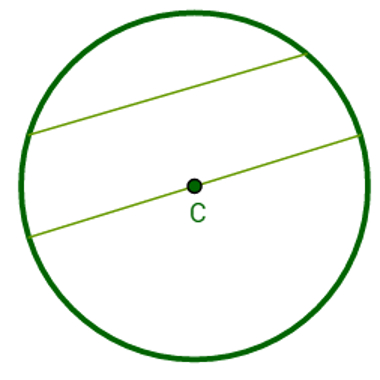
Circunferência contendo um exemplo de corda e um exemplo de diâmetro
Dividindo o comprimento de uma circunferência pelo comprimento de seu raio, o número encontrado sempre será, aproximadamente, 6,28. Dessa maneira, pode-se escrever a seguinte relação:
C = 6,28
r
Dividindo ambos os membros por 2, obtemos o seguinte resultado:
C = 3,14
2r
Esse resultado é o mesmo da divisão anterior, mas realizado com o diâmetro da circunferência no lugar do raio. Dessa maneira, é possível encontrar o comprimento de uma circunferência tendo em mãos apenas o comprimento de seu raio (ou diâmetro). Assim, é possível definir a fórmula para o comprimento da circunferência:
C = 2πr, em que π é aproximadamente 3,14
O mesmo se aplica ao cálculo do comprimento ou perímetro de um círculo. Contudo, não é possível calcular a área de uma circunferência. A área que é calculada, na realidade, é a área do círculo, e a fórmula utilizada para isso é a seguinte:
A = π.r2

Últimas notícias
Outras matérias


















