Classificação de triângulos
A classificação de triângulos é um ponto muito relevante no estudo dessa forma geométrica, que possui três vértices, três lados e três ângulos internos e externos. A fim de facilitar o estudo acerca desse polígono, vamos classificá-lo em relação ao tamanho dos lados (equilátero, isósceles e escaleno) e às medidas de seus ângulos internos (retângulo, acutângulo e obtusângulo). Ao classificá-lo, vamos estudar também algumas propriedades que facilitam as resoluções de problemas.

Classificação dos triângulos quanto aos lados
Podemos classificar um triângulo de acordo com a medida de seus lados. Temos três possíveis combinações em relação ao tamanho dos lados: ou todos os lados são iguais, ou dois lados são iguais e um diferente, ou todos os lados são diferentes.
-
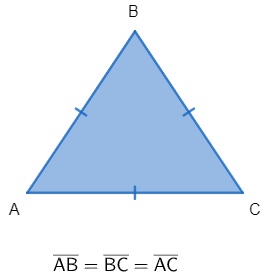
Triângulo equilátero
O triângulo equilátero possui todos os lados congruentes, isto é, todos os lados do triângulo possuem a mesma medida.
-
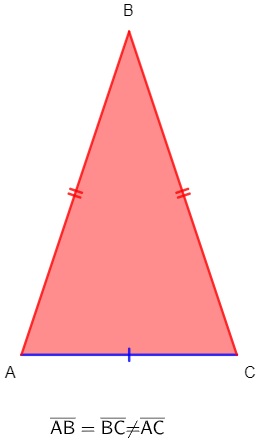
Triângulo isósceles
O triângulo isósceles possui pelo menos dois lados congruentes, ou seja, possui dois lados iguais e um diferente.
-
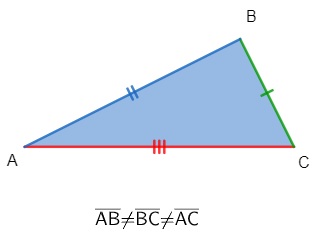
Triângulo escaleno
O triângulo escaleno possui todos os seus lados diferentes, ou seja, cada lado tem uma medida diferente.
Classificação dos triângulos quanto aos ângulos
-
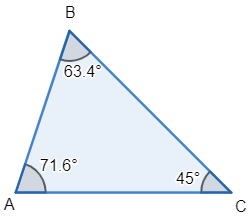
Triângulo acutângulo
O triângulo acutângulo possui todos os seus ângulos internos menores que 90°, ou seja, a medida de cada ângulo interno é um ângulo agudo.
-
Triângulo retângulo
O triângulo retângulo apresenta, em um de seus ângulos internos, um ângulo de 90°, ou seja, um ângulo reto. Além disso, é válido destacar que o lado oposto ao ângulo reto é chamado de hipotenusa e os demais lados são chamados de catetos. Nesse triângulo, é válido o teorema de Pitágoras.
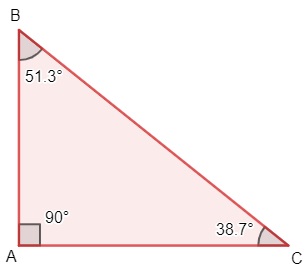
-
Triângulo obtusângulo
O triângulo obtusângulo possui um dos seus ângulos internos com medida maior que 90° e menor que 180°, ou seja, um ângulo obtuso.
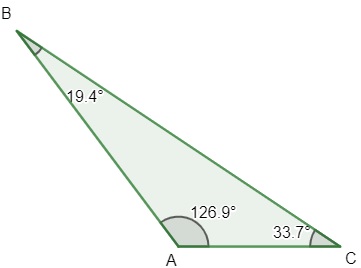
Leia também: Área do triângulo: fórmula e exemplos
Propriedade dos triângulos
-
Propriedade 1: Em qualquer triângulo, a soma dos ângulos internos é sempre igual a 180°.
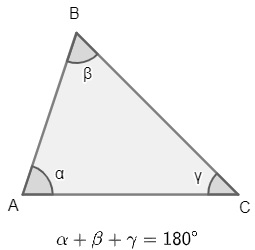
Exemplo
Vamos determinar a medida dos ângulos de um triângulo retângulo com dois ângulos agudos iguais.
Como temos um triângulo retângulo, logo um de seus ângulos é igual a 90°. Como os demais ângulos agudos são iguais, podemos chamá-los de x. Sabemos também que a soma dos ângulos internos de qualquer triângulo é igual a 180°, assim:
90° + x + x = 180°
2x = 180° – 90°
2x = 90°
x = 45°
-
Propriedade 2: Os ângulos internos de um triângulo equilátero são todos iguais a 60°.
Exemplo
Suponha que os valores dos ângulos internos sejam desconhecidos. Assim, chamaremos todos de x, uma vez que o triângulo é equilátero. Como a soma dos ângulos internos é sempre igual a 180°, temos:
x + x + x = 180°
3x = 180°
x = 60°
- Propriedade 3: A altura (segmento de reta perpendicular a um dos lados do triângulo) a mediana (que divide o lado ao meio) e a bissetriz (que divide um ângulo interno ao meio) coincidem-se no triângulo equilátero.
- Propriedade 4: Os ângulos da base de um triângulo isósceles são congruentes.
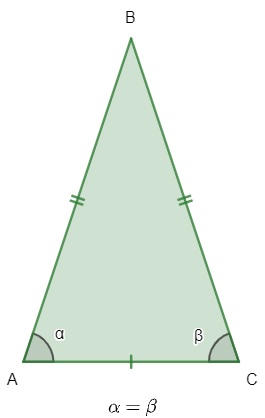
Veja também: Semelhança de triângulos
Exercícios resolvidos
Questão 1 – Determine os valores de x e y sabendo que o triângulo é equilátero.
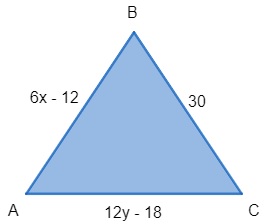
Solução
Como o triângulo é equilátero, todos os seus lados são iguais, assim:
6x – 12 = 30
6x = 30 – 12
6x = 18
x = 3
Por outro lado, temos também que:
12y – 18 = 30
12y = 30 +18
12y = 48
y = 4
Portanto, x = 3 e y = 18.
Artigos Relacionados

Últimas notícias
Outras matérias


















