Classificando um sistema escalonado
Quanto ao estudo dos sistemas lineares, bem sabemos que o foco principal é obter o conjunto solução, quando possível, do sistema a ser estudado. Para obter o conjunto solução, devemos solucionar o sistema linear com algum dos métodos que temos para usar. Um destes métodos é o de escalonamento de um sistema, que consiste em reduzir, equação por equação, a quantidade de incógnitas em cada uma dessas equações.
Quando obtemos um sistema linear escalonado, sem precisar resolvê-lo por completo, apenas analisando as equações escalonadas, podemos concluir com que tipo de sistema, quanto ao seu conjunto solução, iremos trabalhar.
Mas quais são os tipos de classificações para os sistemas lineares?
• SPD – Sistema possível e determinado: sistema no qual é possível determinar o seu conjunto solução e a resposta é única, determinada por apenas um conjunto solução.
• SPI – Sistema possível e indeterminado: sistema no qual é possível determinar vários conjuntos solução. A resposta não é única, por tal fato ele se torna indeterminado.
• SI – Sistema impossível: não existe nenhuma resposta que satisfaça o sistema linear.
Sabendo disso, iremos citar as possibilidades para a análise do sistema escalonado a fim de relacionar esta análise à classificação quanto ao conjunto solução.
No processo de escalonamento, buscamos escrever cada equação com um número de incógnitas menor, e se possível deixar a última equação com apenas uma incógnita. Focando na última equação de um sistema escalonado, podemos retirar todas as informações que precisamos.
Sendo assim, teremos as seguintes possibilidades:
1. Equação do 1° grau com uma incógnita: nesse caso teremos duas possibilidades:
• Coeficiente da incógnita diferente de zero. Exemplo: 8x = 3; 2w = 4; … Em casos como esse, podemos afirmar que o sistema é SPD;
• Coeficiente da incógnita igual a zero. Quando o coeficiente da incógnita for igual a zero, deveremos analisar qual é o valor do termo independente, pois ele ditará qual será o conjunto solução de nosso sistema. Existem duas possibilidades que devem ser analisadas quanto ao termo independente: ele igual a zero e ele diferente de zero.
• Termo independente igual a zero: nesse caso diremos que nosso sistema é SPI, pois qualquer valor para a incógnita irá satisfazer a equação, veja só:
0x=0 substitua valores para a incógnita x. Veja que sempre o resultado será zero, ou seja, essa equação sempre será verdadeira. Em casos como esse, diremos que temos uma incógnita livre, que pode assumir qualquer valor, portanto atribuiremos um valor variável para ela através de uma letra qualquer.
• Termo independente diferente de zero: nesse caso o sistema será SI, pois nunca encontraremos um número que multiplicado por zero resulte em um número que não seja zero. Vamos analisar um exemplo:
0w = 3. Note que qualquer valor substituído no lugar da incógnita, terá como resultado: 0 = 3, uma igualdade falsa, ou seja, não existe solução para esta equação, fazendo com que o sistema não tenha solução.
2. Igualdade verdadeira sem incógnitas: o sistema será SPI. Exemplos: 2 = 2; 3 = 3; 0 = 0;... Note que o terceiro exemplo pode ser relacionado ao primeiro caso no qual o coeficiente da incógnita e o termo independente são zero.
3. Igualdade falsa sem incógnitas: o sistema será SI. Exemplos: 2 = 3; 0 = 9; 0 = 2; 0 = 1.
Vejamos alguns exemplos:
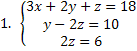
Note que o sistema está completamente escalonado e na última equação do sistema temos uma equação do 1° grau que pode ser resolvida. Sendo assim, esse é um sistema possível e determinado (SPD).
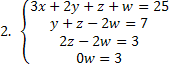
Sistema 4x4 (quatro equações e quatro incógnitas), completamente escalonado. Ao analisar a última equação do sistema, deparamo-nos com um caso de sistema impossível, pois qualquer que seja o valor da incógnita w, ele não irá satisfazer a equação.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática

Últimas notícias
Outras matérias


















