Equação geral de retas perpendiculares
Na geometria analítica temos os conceitos geométricos relacionados com a álgebra. Bem, sabemos, pela geometria, que duas retas são ditas perpendiculares se e somente se elas formarem entre si um ângulo reto (90°). Contudo, na geometria analítica podemos determinar essa perpendicularidade relacionando o coeficiente angular das duas retas. Na geometria analítica é possível obter esse coeficiente angular analisando apenas a equação da reta.
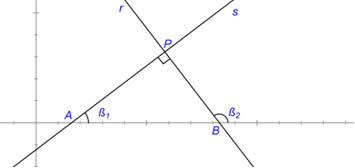
Como dito anteriormente, podemos obter os coeficientes angulares analisando a equação da reta, portanto, vejamos:
.jpg)
Diante disso, podemos determinar a equação da reta tangente a uma reta, desde que conheçamos a equação que determina essa reta. Vejamos um exemplo.
Exemplo 1) Determine a equação geral da reta s que passa pelo ponto (3,2) e é perpendicular à reta r: y=x+2
Resolução: Temos que o coeficiente angular da reta r é igual a 1.
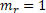
Sabemos que a reta s é perpendicular à reta r, portanto, temos que:

Pela equação geral da reta temos:

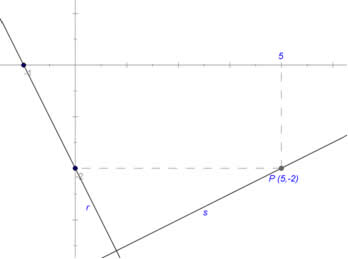
Exemplo 2) Considerando o gráfico abaixo, determine a reta tangente em relação à reta r que passa pelo ponto P (5,-2).
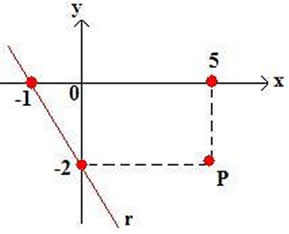
Primeiramente devemos obter a equação da reta r.
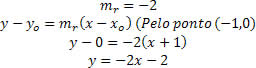
Para determinar a equação da reta s (reta perpendicular à reta r), é necessário obter apenas o coeficiente angular desta reta, pois a coordenada do ponto já é conhecida.

Artigos Relacionados

Últimas notícias
Outras matérias


















