Congruência de triângulos
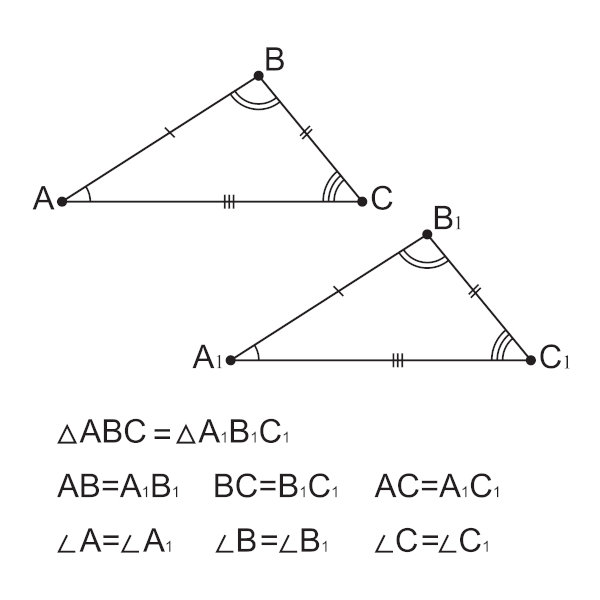
Conhecemos dois triângulos como triângulos congruentes quando eles possuem todas as medidas iguais, tanto para os ângulos quanto para os lados. Para identificar se dois triângulos são congruentes, analisamos o que conhecemos como casos de congruência de triângulo. São conhecidos quatro casos de congruência de triângulo:
-
Lado, Lado, Lado (L, L, L);
-
Lado, Ângulo, Lado (LAL);
-
Ângulo, Lado, Ângulo (ALA);
-
Lado, Ângulo, Ângulo oposto (LAAo).
Leia também: Triângulo retângulo – o triângulo que apresenta um lado medindo 90°
Resumo sobre congruência de triângulos
-
Dois triângulos são congruentes, quando, ao compará-los, os ângulos internos e os lados possuem as mesmas medidas.
-
Existem quatro casos possíveis para identificarmos se os triângulos são semelhantes, são eles:
-
Lado, Lado, Lado (LLL): se os lados forem congruentes, então, os triângulos são congruentes;
-
Lado, Ângulo, Lado (LAL): se dois lados e o ângulo formado entre esses lados são congruentes, então, os triângulos são congruentes;
-
Ângulo, Lado, Ângulo (ALA): se dois ângulos são congruentes e o lado que está entre eles também é congruente, então, esses triângulos são congruentes.
-
Lado, Ângulo, Ângulo oposto (LAAo): se um lado é congruente, o ângulo adjacente a esse lado e o ângulo oposto a esse lado são congruentes, então, os triângulos são congruentes.
-
O que são triângulos congruentes?
Definimos dois triângulos como congruentes quando é possível perceber uma correspondência de igualdade entre as medidas dos lados e dos ângulos desses triângulos, ou seja, dois triângulos são congruentes quando os lados e ângulos correspondentes possuem as mesmas medidas.
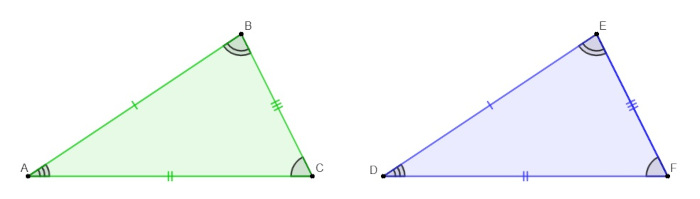
Analisando a imagem, os triângulos são congruentes pelo fato de os lados e ângulos correspondentes possuírem as mesmas medidas.
Analisando os lados, temos que:
AB = DE
AC = DF
EF = BC
Quando analisamos os ângulos, temos que:
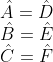
Como todas as medidas são congruentes, então, esses triângulos são congruentes, assim, utilizamos a seguinte notação para representar essa congruência: ΔABC ≡ ΔDEF (lê-se: triângulo a, b, c é congruente ao triângulo d, e, f)
Observação: quando utilizamos essa notação, a ordem dos vértices é relevante. Quando escrevemos dessa maneira, significa que o vértice A é correspondente ao vértice D, que o vértice B corresponde ao vértice E, e que o vértice C é correspondente ao vértice F.
Veja também: Como estudar geometria para o Enem?
Casos de congruência de triângulos
Para identificar se os triângulos são congruentes, não precisamos comparar todos os seus ângulos e lados, pois existem o que conhecemos como casos de congruência, em que três elementos são o suficiente para dizermos se os triângulos são congruentes. Existem quatro casos de congruência, são eles:
-
1º caso de congruência: Lado, Lado, Lado (LLL)
-
2ºcaso de congruência: Lado, Ângulo, Lado (LAL)
-
3º caso de congruência: Ângulo, Lado, Ângulo (ALA)
-
4º caso de congruência: Lado, Ângulo, Ângulo oposto (LAAo)
→ 1º caso de congruência
Ao comparar dois triângulos, se as medidas dos três lados de um deles forem congruentes às medida dos três lados do outro triângulo, então, essa condição é o suficiente para afirmarmos que esses triângulos são congruentes.
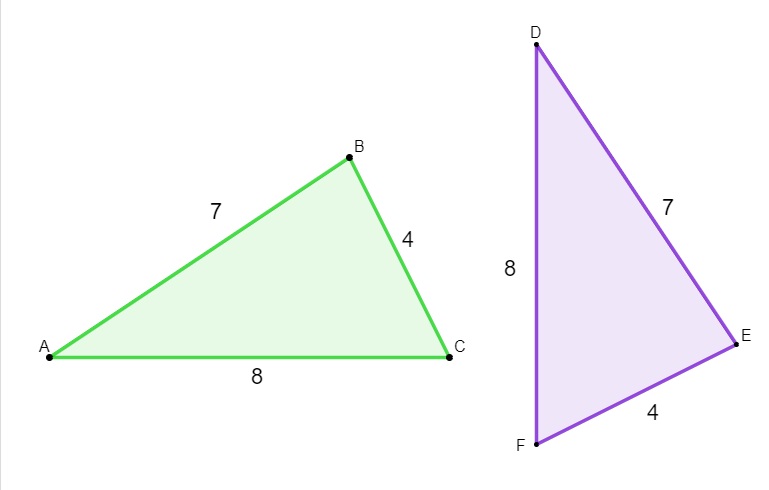
Ao analisar os lados, temos que:
AB = DE
AC = DF
BC = EF
Como os três lados são congruentes, então, esses triângulos são congruentes pelo caso (LLL).
ΔABC ≡ ΔDEF
→ 2º caso de congruência
Dados dois triângulos, se, ao comparar a medida dos lados e dos ângulos, caso haja um lado, um ângulo e um lado congruentes, então, podemos afirmar que esses dois triângulos são congruentes. É importante que a ordem seja respeitada, então, nesse caso, o ângulo precisa estar necessariamente entre os dois lados.
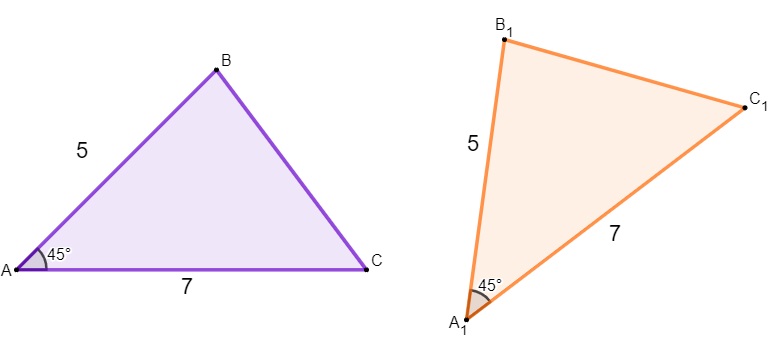
Analisando os dois triângulos, temos que:
AB = A1B1
 = Â1
AC = A1C1
Então, esses triângulos são congruentes pelo caso (LAL).
ΔABC ≡ ΔA1B1C1
→ 3º caso de congruência
Comparando dois triângulos, se dois ângulos são congruentes e o lado que está entre esses ângulos também é congruente, então, esses triângulos são congruentes. Assim como no caso anterior, a ordem é importante, ou seja, o lado congruente tem que estar entre os dois ângulos.
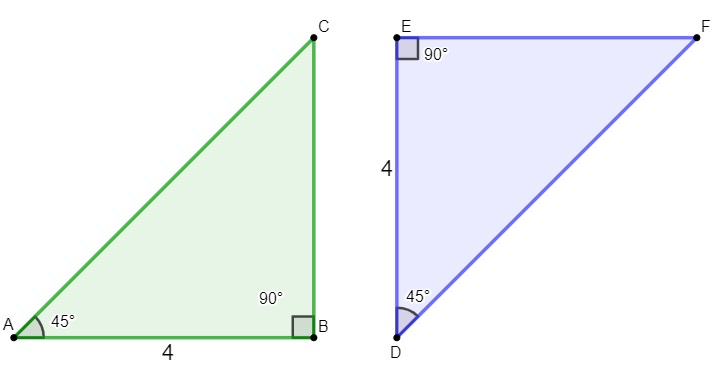
Quando comparamos esses triângulos, temos que:
AB = DE
Eles estão entre os ângulos de 45º e 90º nos dois triângulos, logo, eles são congruentes pelo caso ALA. Assim:
ΔABC ≡ ΔDEF
![]()
→ 4º caso de congruência
Ao compararmos dois triângulos quando eles possuem um lado, um ângulo adjacente a esse lado e um ângulo oposto a esse lado congruentes, sabemos, desse modo, que os triângulos são congruentes.
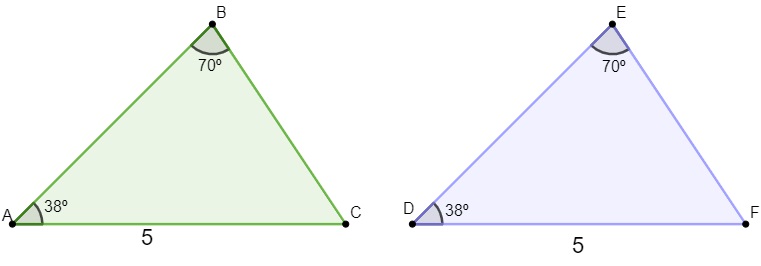
Comparando os triângulos, temos que:
AC = FD
Em ambos, conhecemos um ângulo adjacente e um ângulo oposto a ele, logo, esses triângulos são congruentes pelo caso (LAAo).
ΔABC ≡ ΔDEF
Veja também: Quais são as diferenças entre figuras planas e espaciais?
Propriedades da congruência de triângulos
Existem três propriedades para a congruência, pois ela é reflexiva, simétrica e transitiva.
-
Reflexiva: todo triângulo é congruente a ele mesmo.
-
Transitiva: se o triângulo ABC é congruente ao triângulo A1B1C1 e ao triângulo A2B2C2, então, o triângulo A1B1C1 é congruente ao triângulo A2B2C2.
-
Simétrica: se o triângulo ABC é congruente ao triângulo A1B1C1, então, o triângulo A1B1C1 é congruente ao triângulo ABC.
Exercícios resolvidos sobre congruência de triângulos
Questão 1 - Sobre a congruência de triângulos, julgue as afirmativas a seguir:
I – Ao comparar dois triângulos, se a medida dos ângulos for congruente, então, podemos afirmar que esses triângulos são congruentes pelo caso Ângulo, Ângulo e Ângulo.
II – Dois triângulos equiláteros podem não ser congruentes.
III – Ao comparar dois triângulos, as medidas dos lados forem congruentes um a um, então, podemos afirmar que esses triângulos são congruentes.
Marque a alternativa correta:
A) Somente a I é verdadeira.
B) Somente a II é verdadeira.
C) Somente a III é verdadeira.
D) Somente a II é falsa.
E) Somente a I é falsa.
Resolução
Alternativa E
I – (Falsa) Ter os ângulos congruentes não é o suficiente para que esses triângulos sejam congruentes.
II – (Verdadeira) Quando comparamos dois triângulos equiláteros, eles podem não ser congruentes.
III – (Verdadeira) Esse é o caso de congruência (LLL).
Questão 2 - Na imagem a seguir, sabemos que AB = 15, DC = 10, AC = 3x – 2 e DE = 4y + 3, então, o valor de x + y é igual a:
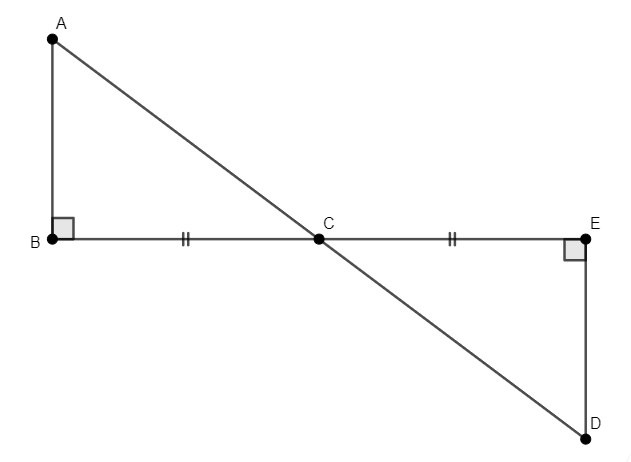
A) 4
B) 5
C) 6
D) 7
E) 8
Resolução:
Alternativa D
Analisando os triângulos ABC e DEC, podemos afirmar que eles são congruentes pelo caso ALA, pois, no vértice C comum aos dois triângulos, o ângulo é o mesmo, além do ângulo que já conhecemos e do lado entre esses ângulos.
Como eles são congruentes, temos que:
AC = DC
3x – 2 = 10
3x = 10 + 2
3x = 12
x = 12 : 3
x = 4
DE = AB
4y + 3 = 15
4y = 15 – 3
4y = 12
y = 12 : 4
y = 3
Por fim: x + y = 4 + 3 = 7
Artigos Relacionados

Últimas notícias
Outras matérias


















