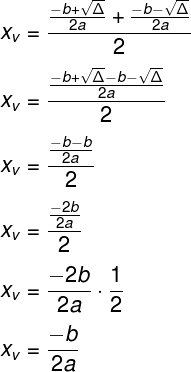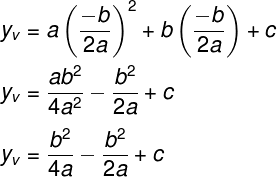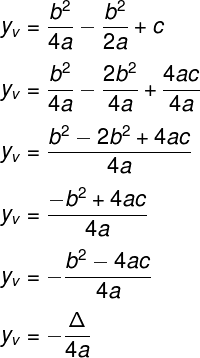Demonstração das fórmulas das coordenadas do vértice
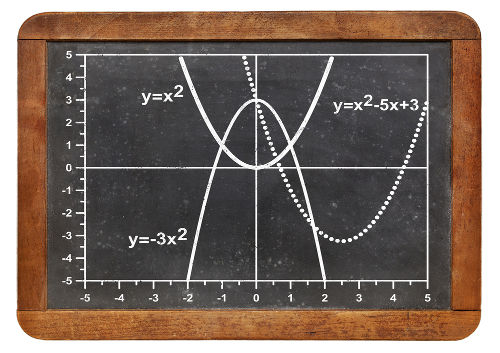
Toda parábola pode ser usada como representação geométrica de alguma função na forma f(x) = ax2 + bx + c, que é chamada de função do segundo grau. Toda função do segundo grau pode possuir a concavidade voltada para cima, e consequentemente um ponto de mínimo, ou a concavidade voltada para baixo, e consequentemente um ponto de máximo. Esse ponto de mínimo (ou de máximo) é chamado de vértice da parábola.
Seja V o vértice de uma parábola e (xv, yv) suas coordenadas, as fórmulas usadas para encontrar essas coordenadas são:
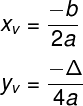
Para demonstrar essas fórmulas, é necessário conhecer uma outra técnica que também pode ser usada pra encontrar as coordenadas do vértice.
Coordenadas do vértice
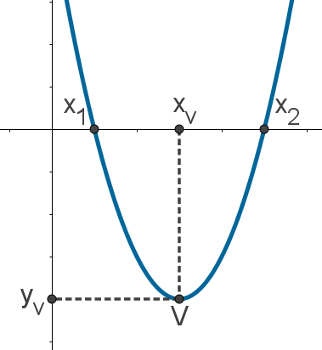
Observe os pontos em destaque, vértice e raízes, na figura a seguir.
Perceba que a coordenada x do vértice (xv) fica no ponto médio do segmento entre as raízes da parábola, portanto, para encontrar a coordenada xv, podemos calcular a média aritmética entre as raízes da função:
![]()
Note também que a imagem da função aplicada no ponto xv é justamente yv, ou seja, f(xv) = yv.
Tendo essas informações como base, podemos realizar alguns cálculos simples para encontrar as fórmulas usadas para calcular xv e yv.
Demonstrações das fórmulas
Dada a função f(x) = ax2 + bx + c, podemos usar a fórmula de Bháskara para determinar as fórmulas de xv e yv. Sabendo que as raízes de uma função do segundo grau podem ser encontradas da seguinte maneira:
.jpg)
Logo,
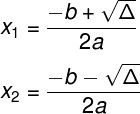
Lembre-se de que:
![]()
Podemos, então, substituir os valores de x1 e x2 para encontrar:
Que é justamente a fórmula usada para determinar xv.
A fórmula usada para determinar yv pode ser obtida ao encontrar a imagem da função no ponto xv:
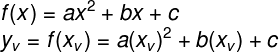
Substituindo o valor de xv, temos:
Para finalizar, basta fazer o procedimento adequado de adição (e subtração) de frações. Esse procedimento depende do mínimo múltiplo comum.
Artigos Relacionados

Últimas notícias
Outras matérias