Equação-Produto
Na fatoração algébrica aprendemos a escrever expressões algébricas na forma de um produto de expressões algébricas. Essa finalidade serve para o estudo da equação-produto, em que será analisada cada expressão, ou ainda, cada polinômio que está envolvido nessa multiplicação, de modo a determinar os valores que satisfazem a equação.
Antes de adentrarmos nas equações-produto, devemos relembrar uma propriedade bem elementar dos números reais:
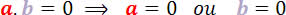
Portanto, como teremos expressões algébricas no lugar dos valores a e b, analisaremos cada expressão algébrica desse produto separadamente, afinal devemos analisar todas as possibilidades em que a equação-produto resultará no valor nulo.
Vejamos um exemplo para melhor compreender o que se passa nas equações-produto.
Exemplo 1) Determine os valores de x que satisfazem a seguinte equação: (x+2).(x-1)=0.
Note que teremos que analisar as seguintes equações:
x+2=0 e x-1=0
• Obtendo o valor da equação x+2=0
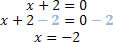
• Obtendo o valor da equação x-1=0
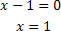
Sendo assim, o conjunto solução da equação-produto (x+2).(x-1)=0 corresponde aos valores {-2,1}.
Como foi visto anteriormente, deveremos apenas solucionar as equações que estão sendo multiplicadas, ao invés de resolvermos aquela multiplicação e posteriormente solucionarmos a nova equação, pois veja como ficaria se multiplicássemos as duas equações:
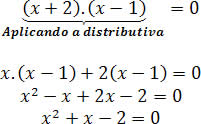
Veja outro exemplo:
Exemplo 2) Determine a solução da equação-produto a seguir:

Devemos analisar as equações separadamente:
Na equação x2-4=0, temos:
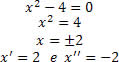
Na equação x2-5x+6=0, temos:
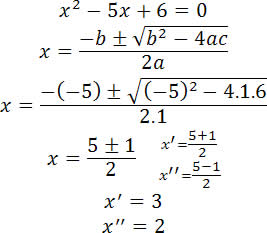
Sendo assim, o conjunto solução é:
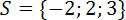

Últimas notícias
Outras matérias


















