Função modular
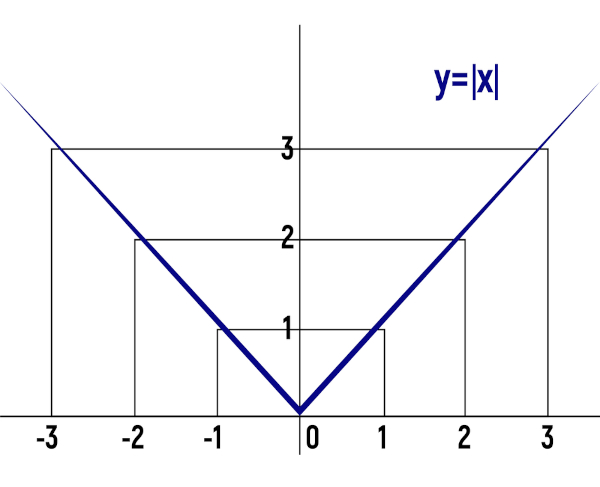
Conhecemos como função modular uma função cuja lei de formação possui uma variável dentro do módulo. O módulo de um número n é representado por |n|, e sabemos que |n| tem como resultado sempre um número positivo. A função modular pode ter diferentes leis de formação, podendo ter dentro do módulo uma equação do 1º grau, 2º grau, entre outros tipos de equações.
Para encontrar o valor numérico de uma função modular, substituímos o valor da variável e, ao final, aplicamos a propriedade do módulo. Podemos também representar o gráfico de uma função modular.
Leia também: Quais as diferenças entre função e equação?
Resumo sobre função modular
-
Uma função é considerada modular quando em sua lei de formação existir pelo menos uma variável dentro do módulo.
-
Para calcular o valor numérico de uma função modular, utilizamos a definição de módulo.
-
Uma função modular pode ter em seu módulo qualquer tipo de equação, sendo as mais comuns do 1º e 2º grau.
O que é uma função modular?
Conhecemos como função modular uma função que possui domínio e contradomínio no conjunto dos números reais, ou seja, f: R → R, e que, em sua lei de formação, exista variável que esteja dentro do módulo.
Exemplos:
-
f(x) = |x|
-
g(x) = |x – 5|
-
h(x) = |-x² – 2x + 3|
Para trabalhar com funções modulares, é importante lembrar a definição de módulo e suas propriedades.
Representamos o módulo de um número n por |n|, e, por definição, temos que:
![]()
O módulo de um número sempre gera resultados positivos, por exemplo:
|2| → como 2 > 0 → |2| = 2
|-2| → como -2 < 0 → |-2| = – (-2) = 2
Propriedades da função modular
Vale lembrar que, em uma função modular, todas as propriedades do módulo são válidas.
Considere a e b como números reais:
-
1ª propriedade: o módulo de um número real é igual ao módulo do seu oposto.
|a| = |-a|
-
2ª propriedade: o módulo do quadrado de a é igual ao módulo de a ao quadrado.
|a²| = |a|²
-
3ª propriedade: o módulo de um produto é igual ao produto dos módulos.
|a · b| = |a| · |b|
-
4ª propriedade: o módulo da soma é menor ou igual à soma dos módulos.
|a + b| ≤ |a| + |b|
-
5ª propriedade: o módulo da diferença é maior ou igual à diferença dos módulos.
|a – b| ≥ |a| – |b|
Veja também: Quais são as propriedades da função exponencial?
Valor numérico de uma função modular
Para calcular o valor numérico de uma função modular, basta substituir a variável x pelo valor desejado e resolver a expressão. Durante a resolução, é sempre necessário aplicar a definição do módulo.
Exemplo:
f(x) = |-x² – 5x + 1|
a) x = 2
f(2) = |-2² – 5 · 2 + 1|
f(2) = |-4 – 10 + 1|
f(2) = |-13|
f(2) = 13
b) x = -3
f(-3) = |– (-3)² – 5 (-3) + 1|
f(-3) = |-9 + 15 + 1|
f(-3) = |7|
f(-3) = 7
Gráfico de uma função modular
Para construir o gráfico da função modular, é importante perceber que a função possui comportamento diferente quando o que está dentro do módulo for positivo e quando for negativo.
Exemplo 1:
Começando pelo exemplo mais simples possível de função modular, construiremos o gráfico da função.
f(x) = |x|
Existem duas possibilidades para a função:
![]()
Para construir o gráfico, escolheremos alguns valores numéricos para essa função:
|
x |
f(x) = |x| |
(x, y) |
|
-2 |
f(-2) = |-2| = 2 |
A (-2, 2) |
|
-1 |
f(-1) = |-1| = 1 |
B (-1, 1) |
|
0 |
f(0) = |0| = 0 |
C (0, 0) |
|
1 |
f(1) = |1| = 1 |
D (1, 1) |
|
2 |
f(2) = |2| = 2 |
E (2, 2) |
Agora faremos a representação desses pontos no gráfico.

Exemplo 2:
f(x) = |x² – 6x + 8|
1º passo: encontrar os zeros da função.
Para que |x² – 6x + 8| = 0 → x² – 6x + 8 = 0
Calculando delta e bhaskara, temos que:
x² – 6x + 8 = 0
a = 1
b = -6
c = 8
Δ = b² – 4ac
Δ = (-6)² – 4 · 1 · 8
Δ = 36 – 32
Δ = 4
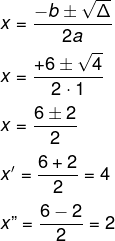
Então, temos os pontos A(4, 0) e B(2, 0).
2º passo: encontrar xv e yv.
O xv pode ser encontrado somando x’ e x’’ e dividindo por 2.
xv = (4 + 2) : 2
xv = 6 : 2
xv = 3
Para calcular o yv, basta substituir 3 na função:
f(x) = |x² – 6x + 8|
f(3) = |3² – 6 · 3 + 8|
f(3) = |9 – 18 + 8|
f(3) = |-1|
f(3) = 1
Então, o vértice V possui coordenadas V(3, 1).
3º passo: encontrar o ponto de intersecção da parábola com o eixo y.
Para isso, basta calcular f(0):
f(x) = |x² – 6x + 8|
f(0) = |0² – 6 · 0 + 8|
f(0) = |8|
f(0) = 8
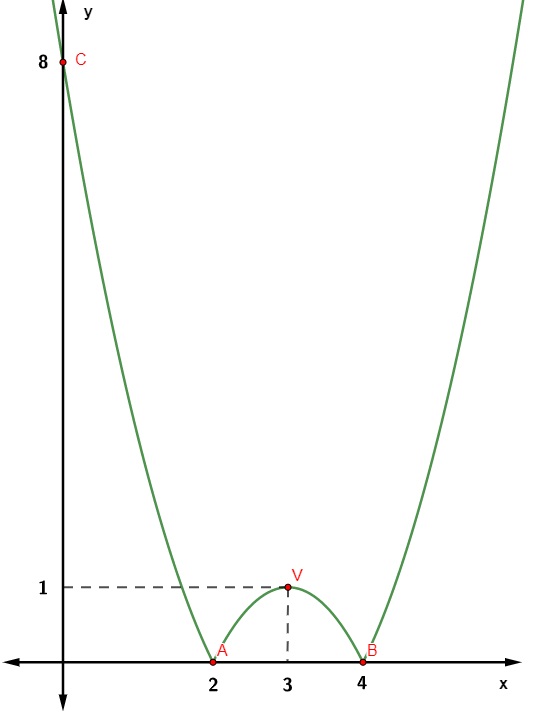
Por fim, o ponto C(0, 8) pertence ao gráfico.
Marcando os pontos A, B, C e V no gráfico, temos o seguinte:
Leia também: 5 passos para construir um gráfico de uma função de 2º grau
Exercícios resolvidos sobre função modular
Questão 1 - (IBFC) Considere a função f(x) = |x² – 5|, cujo domínio é o conjunto dos números naturais. Assinale a alternativa que indica qual o menor conjunto que pertencerá o contradomínio dessa função.
A) Números naturais
B) Números inteiros
C) Números racionais
D) Números reais
E) Números complexos
Resolução
Alternativa A
Como o domínio é o conjunto dos números naturais, então, x sempre será um número natural.
Um número natural ao quadrado (x²) também é um número natural. Quando calculamos a diferença desse x² com 5, e calculamos o módulo, ou seja |x² – 5|, o resultado também será um número natural, pois o módulo de um número é sempre positivo. Sendo assim, o menor conjunto possível para o contradomínio é o conjunto dos números naturais.
Questão 2 - Seja f(x) = |2x + 2|, existem dois valores a e b, tal que a ≠ b, mas f(a) = f(b) = 4. Então, o valor de f(a + b) é igual a:
A) -2
B) -1
C) 0
D) 1
E) 2
Resolução
Alternativa E
Dada a função f(x) = |2x + 2|, sabemos que f(a) = 4 e f(b) = 4, mas que a ≠ b.
Então, temos que:
f(x) = |2x + 2| = 4
Existem dois casos em que f(x) seja igual a 4. Aplicando a definição de módulo, temos que:
f(x) = 4 → 2x1 + 2 = 4 ou 2x2 + 2 = -4
Então, temos que:
Seja x1 = a:
2a + 2 = 4
2a = 4 – 2
2a = 2
a = 2 : 2
a = 1
Seja x2 = b:
2b + 2 = -4
2b = -4 – 2
2b = -6
b = -6 : 2
b = -3
Queremos o valor de f(a + b) = f(1 + (-3)) = f(-2):
f(x) = |2x + 2|
f(-2) = |2 · (-2) + 2|
f(-2) = |-4 + 2|
f(-2) = |-2|
f(-2) = 2
Artigos Relacionados

Últimas notícias
Outras matérias


















