Função sobrejetora
A função sobrejetora é um caso particular de função. Denomina-se função a relação entre dois conjuntos na qual o domínio (primeiro conjunto) sempre possui um correspondente no contradomínio (segundo conjunto). Uma função é classificada como sobrejetora quando o conjunto imagem é igual ao contradomínio da função, o que significa que todos os elementos do contradomínio estão relacionados a um elemento do domínio.
Saiba também: Domínio, contradomínio e imagem de uma função — qual a importância desses conjuntos?
Resumo sobre função sobrejetora
- Função sobrejetora é um caso particular de função.
- A função é sobrejetora quando o contradomínio é igual ao conjunto imagem da função.
- Se todos os elementos do contradomínio estiverem relacionados a pelo menos um elemento do domínio, a função é sobrejetora.
- A função afim é um exemplo de função sobrejetora, e a função quadrática é um exemplo de função não sobrejetora.
- Uma função também pode ser injetora ou bijetora.
O que é uma função sobrejetora?
A função sobrejetora, conhecida também como função sobrejetiva, é um caso particular de função. Uma função é classificada como sobrejetora quando todos os elementos do contradomínio são imagens de um ou mais elementos do domínio, ou seja, quando o conjunto imagem da função é igual ao seu contradomínio.
Exemplos de função sobrejetora
- Exemplo 1:
Sendo f: A → B
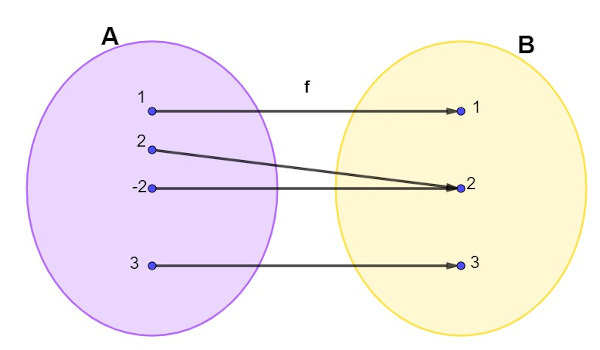
Note que todos os elementos de B são imagens de um elemento no conjunto A. Logo, o contradomínio é igual à imagem da função.
- Exemplo 2:
As funções polinomiais do 1º grau, conhecidas também como funções afins, com domínio e contradomínio no conjunto dos números reais, são sempre funções sobrejetoras, pois a imagem da função é também igual ao conjunto dos números reais.
Considerando a função afim com lei de formação f(x) = 2x + 1, sabe-se que para qualquer número real y existirá um valor de x tal que f(x) = y.
Veja também: Função logarítmica — a função inversa da função exponencial
Exemplos de função não sobrejetora
- Exemplo 1:
Sendo f: A → B
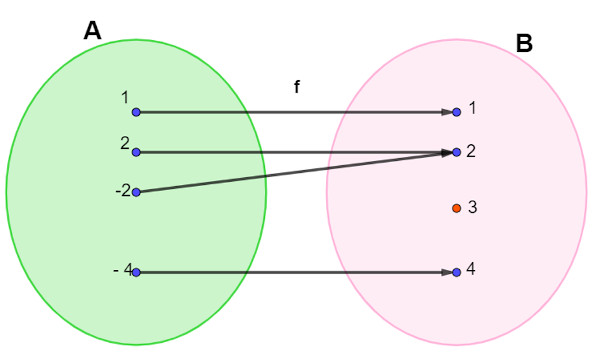
Perceba que no contradomínio existe um elemento que não é imagem de nenhum elemento do domínio. Assim, essa função não é sobrejetora, pois o contradomínio não é igual ao conjunto imagem.
Formalmente, dizemos que a função f: A → B é uma função injetora se e somente se
∀ y ϵ B, ∃ x | f(x) = y
Isso quer dizer que para todo y pertencente ao conjunto B existe um x tal que a imagem de x é y.
- Exemplo 2:
As funções quadráticas, conhecidas também como funções polinomiais do 2º grau, não são sobrejetoras, pois seu conjunto imagem não é igual ao contradomínio.
Considerando a função quadrática com lei de formação f(x) = x², sabe-se que para y = -2 não existe nenhum valor real de x tal que f(x) = y, logo essa função não é sobrejetora.
Gráfico de função sobrejetora
Ao analisar o gráfico de uma função, é possível perceber que ela é sobrejetora quando sua imagem é igual ao contradomínio. Vejamos, por exemplo, o gráfico desta reta:
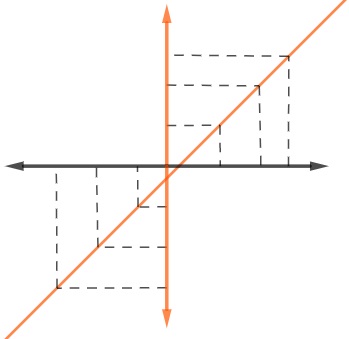
Perceba que todo elemento do eixo y é imagem de um elemento no eixo x, logo essa função é sobrejetora.
Saiba mais: Qual é a relação entre os coeficientes e o gráfico de uma função do segundo grau?
Diferença entre função injetora, sobrejetora e bijetora
Além da função sobrejetora, em que o domínio da função é igual ao seu conjunto imagem, uma função pode ser classificada como injetora ou bijetora.
- Função injetora: a função é considerada injetora quando existe um único valor de x tal que f(x) = y considerando um elemento y pertencente à imagem da função.
- Função bijetora: a função é considerada bijetora se ela é sobrejetora e injetora simultaneamente.
→ Videoaula sobre função injetora, sobrejetora e bijetora
Exercícios resolvidos sobre função sobrejetora
Questão 1
Dados os conjuntos A = {-2, 0, 1, 2} e B = {0, 1, 4} e considerando f: A → B, julgue as afirmativas abaixo:
I. Se f(x) = x², a função é sobrejetora.
II. Se f(x) = | |x | - 1 |, a função é sobrejetora.
Marque a alternativa correta:
- Somente I é verdadeira.
- Somente II é verdadeira.
- Ambas são verdadeiras.
- Ambas são falsas.
Resolução:
Alternativa A
I. Verdadeira
Dada a função f(x) = x², temos que:
f(-2) = (-2)² = 4
f(0) = 0² = 0
f(1) = 1² = 1
f(2) = 2² = 4
Note que a imagem da função é o conjunto im(f) = {0, 1, 4}, que é igual ao conjunto B, logo essa função é sobrejetora.
II. Falsa
Dada a função f(x) = | |x| - 1|, temos que:
f(-2) = | |-2| - 1| = |2 – 1| = | 1 | = 1
f(0) = | |0| - 1| = |0 – 1| = | - 1| = 1
f(1) = | |1| - 1| = | 1 – 1 | = |0| = 0
f(2) = | |2| - 1| = |2 -1 | = | 1 | = 1
Então, o conjunto im(f) = {0, 1}.
Note que ele é diferente do contradomínio. Assim, a função não é sobrejetora.
Questão 2
Uma função é sobrejetora quando:
- todos os elementos da imagem são correspondentes de um único elemento no domínio.
- todos os elementos do contradomínio possuem um único elemento correspondente a ele no domínio.
- todos os elementos do contradomínio possuem pelo menos um elemento correspondente a ele no domínio.
- todos os elementos do domínio possuem um correspondente no contradomínio.
- ela é injetora e bijetora ao mesmo tempo.
Resolução:
Alternativa C
A função é sobrejetora se todos os elementos do contradomínio forem correspondentes de pelo menos um elemento do domínio.
Artigos Relacionados

Últimas notícias
Outras matérias


















