Sabemos que em uma reta existem infinitos pontos, com apenas dois desses pontos podemos representar essa mesma reta no plano cartesiano, pois dois pontos distintos sempre serão colineares (pertencerão ou formarão uma reta).

Com o estudo da geometria analítica aprendemos que não é necessário ter dois pontos distintos para formar uma reta, podemos construir uma reta no plano cartesiano conhecendo apenas um de seus infinitos pontos e sabendo o valor do ângulo formado com a reta e o eixo Ox.

Essa outra forma de representarmos uma reta será feita levando em consideração a inclinação da reta e o seu coeficiente angular. Considere uma reta s que intercepta o eixo Ox no ponto M.



A reta s está formando com o eixo Ox um ângulo β. A medida desse ângulo é feita em sentido anti-horário a partir de um ponto pertencente ao eixo Ox. Assim, podemos dizer que a reta s tem inclinação β e o seu coeficiente angular (m) igual a: m = tg β.

A inclinação da reta irá variar entre 0° ≤ β <180°. Veja os exemplos de algumas possibilidades de variação da inclinação da reta e seus respectivos coeficientes angulares:

Exemplo 1:

Nesse exemplo o valor da inclinação é menor que 90º.



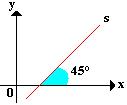
Inclinação igual a 45° e coeficiente angular igual a: m = tg 45° = 1.

Exemplo 2:

Nesse exemplo o valor da inclinação da reta é maior que 90° e menor que 180°.



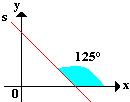
Inclinação igual a 125° e coeficiente angular da reta igual a: m = tg 125° = -2.

Exemplo 3:

Quando a reta for paralela ao eixo Oy, ou seja, tiver uma inclinação igual a 90° o seu coeficiente angular não irá existir, pois não é possível calcular a tg 90°.


Exemplo 4:

Nesse exemplo a reta s é paralela ao eixo Ox, ou seja, seu ângulo de inclinação é igual a 180°, portanto, o seu coeficiente angular será igual a: m = tg 180º = 0.