Inequação-quociente
O estudo das inequações é baseado em determinar um intervalo cuja incógnita satisfaça aquela desigualdade, como bem diz a palavra “inequação”, que dá a ideia de “não igual”.
Na inequação-quociente, tem-se uma desigualdade de funções fracionárias, ou ainda, de duas funções na qual uma está dividindo a outra. Diante disso, deveremos nos atentar ao domínio da função que se encontra no denominador, pois não existe divisão por zero. Com isso, a função que estiver no denominador da inequação deverá ser diferente de zero.
O método de resolução se assemelha muito à resolução de uma inequação-produto, de modo que devemos analisar o sinal das funções e realizar a intersecção do sinal dessas funções. Vejamos alguns exemplos:
1) Resolva a inequação a seguir.
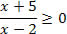
Como o denominador deve ser diferente de zero, podemos afirmar que o valor de x não poderá ser igual a 2.
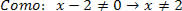
Vamos estudar os sinais das funções.
Função f(x)=x+5
• Zero da função: x=-5
• Sinal do coeficiente a: a=1, valor maior que zero, portanto é uma função crescente.
Sendo assim, analisando os sinais dessa função, temos:
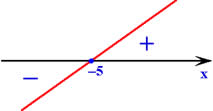
Função: g(x)=x-2
• Zero da função: x=2
• Sinal do coeficiente a: a=1, valor maior que zero, portanto é uma função crescente.
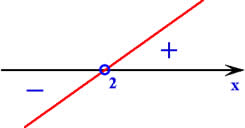
Agora devemos realizar a intersecção dos intervalos das duas funções, lembrando que o ponto 2 é um valor aberto, pois não pertence ao domínio da desigualdade.
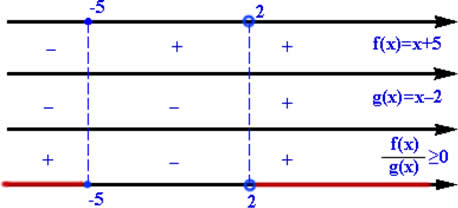
Veja que ao fazer a intersecção das funções deve ser feito também o jogo de sinal, assim como na equação produto. Sendo assim, podemos esboçar o conjunto solução:
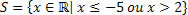
Artigos Relacionados

Últimas notícias
Outras matérias


















