Lei dos cossenos
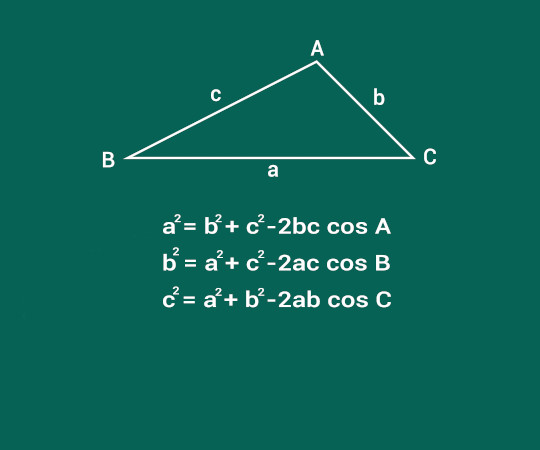
A lei dos cossenos é uma relação entre os lados do triângulo e o cosseno de um dos seus ângulos. Conhecida também como teorema dos cossenos, essa relação é utilizada para encontrar a medida de lados desconhecidos de um triângulo cujos valores de dois lados são conhecidos e o valor de um ângulo interno é conhecido.
Dado um triângulo de lados a, b e c, com o ângulo  conhecido, a fórmula da lei dos cossenos é a² = b² + c² - 2bc cosÂ, ou seja, o comprimento do lado a é igual à soma do quadrado da medida dos lados b e c menos duas vezes o produto da medida dos lados b e c com o cosseno do ângulo oposto ao lado a.
Leia também: Seno, cosseno e tangente — qual a diferença?
Resumo sobre lei dos cossenos
- A lei dos cossenos é uma relação entre a medida dos lados de um triângulo e o cosseno de um dos seus ângulos.
- Utilizamos a lei dos cossenos para encontrar a medida de lados desconhecidos de um triângulo qualquer.
- Dado um triângulo de lados a, b e c, as fórmulas da lei dos cossenos são:
a2=b2+c2−2⋅a⋅b⋅cosÂ
b2=a2+c2−2⋅a⋅c⋅cosˆB
c2=a2+b2−2⋅a⋅b⋅cosˆC
Videoaula sobre lei dos cossenos
O que é a lei dos cossenos?
Conhecida também como teorema dos cossenos, a lei dos cossenos é uma relação entre a medida dos lados de um triângulo e o cosseno de um dos seus ângulos. A lei dos cossenos nos permite descobrir a medida de um lado do triângulo quando conhecemos a medida de outros dois lados e o ângulo oposto ao lado que queremos descobrir.
Qual é a fórmula da lei dos cossenos?
Seja a o lado do qual queremos descobrir o valor e b e c as medidas dos outros dois lados, a lei dos cossenos mostra que o quadrado do lado a é igual à soma dos quadrados dos lados b e c menos duas vezes os lados b vezes o cosseno do ângulo oposto ao lado a.
De modo geral, considerando um triângulo de lados a, b e c, podemos escrever a fórmula da lei dos cossenos de três maneiras:
- a2=b2+c2−2⋅a⋅b⋅cosÂ
- b2=a2+c2−2⋅a⋅c⋅cosˆB
- c2=a2+b2−2⋅a⋅b⋅cosˆC
A fórmula a ser usada depende de qual dos ângulos é conhecido. Se é conhecido o valor do ângulo Â, utilizamos a primeira fórmula; caso seja o ângulo ˆB, a segunda fórmula; por fim, caso seja o ângulo ˆC, a terceira fórmula.
É importante perceber que as fórmulas sempre possuem um mesmo padrão. Logo, sabendo que o lado que fica sozinho na igualdade é o que está oposto ao ângulo conhecido, fica mais fácil saber como devemos aplicar a fórmula.
Quando se aplica a lei dos cossenos?
A lei dos cossenos é utilizada quando conhecemos dois lados e um ângulo do triângulo e queremos encontrar o comprimento do terceiro lado desse triângulo. Normalmente, a lei dos cossenos é aplicada para triângulos não retângulos, ainda que seja válida para triângulos retângulos.
Demonstração e aplicação da lei dos cossenos
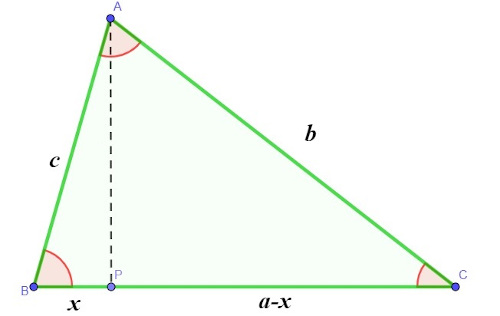
Existem diferentes maneiras de demonstrar a lei dos cossenos. Faremos a seguir a demonstração por semelhança de triângulos. Primeiramente, construiremos o triângulo A, B e C, de lados a, b e c, e traçaremos a altura do vértice A, que será o segmento AP, dividindo a base em duas partes:
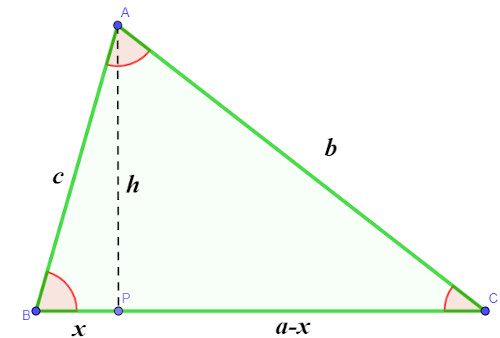
Com o segmento AP, são formados na imagem dois triângulos, o triângulo BPA e o triângulo APC. De início, analisando o triângulo BPA, sabemos que:
cosˆB=xc
Então, temos que:
x=c⋅cosˆB
Aplicando o teorema de Pitágoras no triângulo BPA:
c2=x2+h2
Isolando h:
h2=c2−x2
- Exemplo:
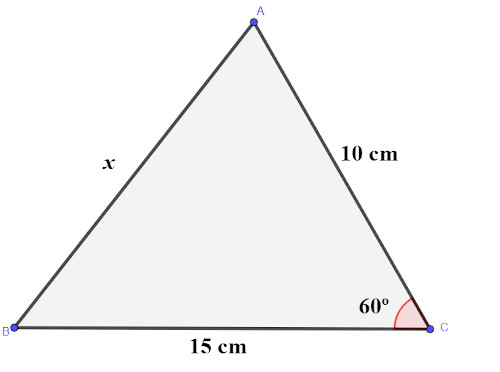
Encontre a medida do lado representada por x na imagem:
Resolução:
Conhecemos o ângulo de 60°, e o lado oposto a ele mede x. Então, substituindo na fórmula da lei dos cossenos, será a incógnita x que ficará sozinha na igualdade:
x2=102+152−2⋅10⋅15⋅cos60°
x2=100+225−2⋅10⋅15⋅12
x2=325−150
x2=175
x=√175
x≈13,2 cm
Aplicando o teorema de Pitágoras no triângulo APC:
b2=h2+(a−x)2
b2=h2+a2−2⋅a⋅x+x2
Sabemos que:
h²=c²−x²
Portanto:
b2=c2−x2+a2−2ax+x2
b2=c2+a2−2ax
Como x = c·cosB:
b2=c2+a2–2·a·c·cosB
Note que nós encontramos a fórmula da lei dos cossenos. Para demonstrar as outras duas fórmulas, o processo é análogo a este, pois se traçarmos as alturas dos outros lados, encontramos as outras duas fórmulas da lei dos cossenos.
Acesse também: Demonstração da lei dos senos
Lei dos cossenos no triângulo retângulo
Durante a aplicação da lei dos cossenos em um triângulo retângulo, basta lembrar que o triângulo retângulo é aquele que possui 90° e que o cosseno de um ângulo de 90° é igual a 0, então temos que:
a2=b2+c2−2⋅a⋅b⋅cos90°
a2=b2+c2−2⋅a⋅b⋅0
a2=b2+c2
Note então que encontramos o teorema de Pitágoras, por isso utilizamos diretamente o teorema de Pitágoras em triângulos retângulos. A lei dos cossenos é interessante para triângulos não retângulos, pois sua aplicação em um triângulo retângulo nada mais é que o teorema de Pitágoras.
Exercícios resolvidos sobre lei dos cossenos
Questão 1
A medida do lado representado por x é igual a:
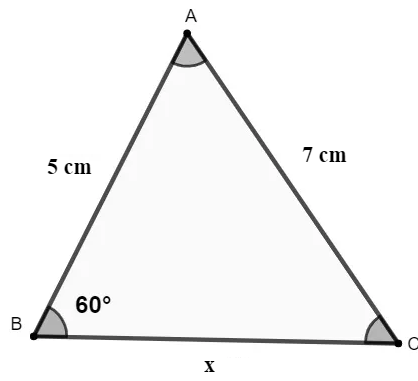
A) 9 cm
B) 8 cm
C) 7 cm
D) 6 cm
E) 6 cm
Resolução:
Alternativa B
Aplicando a lei dos cossenos:
72=52+x2−2⋅5⋅x⋅cos60°
49=25+x2−10⋅x⋅12
49=25+x2−5x
x2−5x+25−49=0
x2−5x−24=0
Calculando as raízes da equação, temos que a = 1, b = -5 e c = -24, logo:
Δ=b2−4ac
Δ=(−5)2−4⋅1⋅(−24)
Δ= 25 +96
Δ=121
Agora, utilizando a fórmula de Bhaskara:
x=−b±√Δ2a
x=5±√1212⋅1
x=5±112
Como há duas soluções, o nosso interesse é somente na solução positiva, já que a resposta é a medida do lado de um triângulo:
x=5+112=162=8
Questão 2
(Uerj — adaptada) Ao coletar os dados para um estudo topográfico da margem de um lago a partir dos pontos A, B e T, um técnico determinou as medidas AT = 32 m, BT = 13 m e AˆTB = 120°, representadas no esquema abaixo:
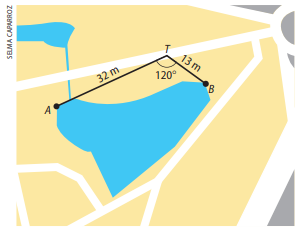
Calculando a distância, em metros, entre os pontos A e B, definidos pelo técnico nas margens desse lago, a distância é de, aproximadamente:
A) 38 metros
B) 39 metros
C) 40 metros
D) 41 metros
E) 42 metros
Resolução:
Alternativa C
Aplicando a lei dos cossenos:
x2=322+132−2⋅32⋅13⋅cos 120°
x2=1024+169−2⋅32⋅13⋅(−12)
x2=1193+416
x2=1609
x=√1609
x≈40,1