Matriz inversa
Conhecemos como matriz inversa de A a matriz A-1, tal que, quando multiplicamos as matrizes A e A-1, temos como produto a matriz identidade In, ou seja, A × A-1 = In. Para encontrar uma matriz inversa de uma matriz cujos elementos são conhecidos, utilizamos igualdade do produto de duas matrizes, encontrando os termos da matriz inversa por meio de uma equação.
No estudo da matriz inversa, existem propriedades importantes. Um exemplo é que uma matriz quadrada só possuirá uma matriz inversa se, e somente se, o seu determinante for diferente de zero.
Leia também: O que é uma matriz simétrica?
Matriz identidade
Antes de entender o que é uma matriz inversa, é essencial compreender o que é a matriz identidade. Trata-se de uma matriz quadrada cujos elementos da diagonal principal são iguais a 1 e os demais elementos são iguais a 0.
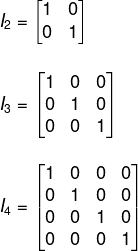
A matriz identidade é o elemento neutro da multiplicação de matrizes, ou seja, seja A uma matriz quadrada de ordem n, então A · In = A.
Como calcular a matriz inversa
Quando estudamos os números reais, sabemos que o inverso de um número n é o número n-1, tal que o produto entre os dois é igual a 1, ou seja, o elemento neutro da multiplicação. Esse conceito se relaciona diretamente com o de matriz inversa.
A matriz inversa de A é a matriz A-1, tal que o produto entre a matriz e sua inversa seja igual a In. Para encontrar a matriz inversa de A, vamos montar a matriz com incógnitas, tal que: A·A-1 = In.
Exemplo 1:
Encontre a matriz inversa de A.
![]()
Para encontrar a matriz inversa de A, temos que:
![]()
Então, pela definição de matriz inversa, chegamos a:
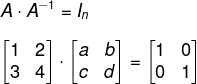
Realizando a multiplicação:
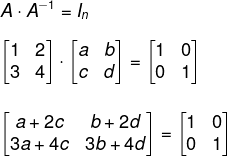
Realizando a igualdade matricial, sabemos que duas matrizes são iguais quando cada um dos seus termos são iguais. Sendo assim, é possível dividir essa situação em dois sistemas de equações. Analisando a primeira coluna, temos que:
![]()
Agora basta resolver o sistema de equações, isolando a segunda equação e substituindo na primeira:
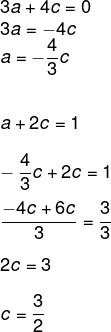
Como encontramos o valor de c=3/2, agora é possível encontrar o valor de a, substituindo na primeira equação:
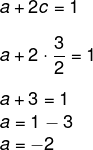
Analisando a segunda coluna das duas matrizes, vamos encontrar o valor de b e d com o segundo sistema:
![]()
Na primeira equação, temos que:
b + 2d = 0
b = -2d
Substituindo na segunda equação:
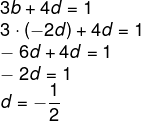
Para encontrar o valor de b, substituiremos o valor de d na primeira equação:
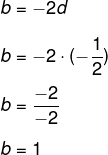
Agora que conhecemos o valor de cada uma das incógnitas, é possível representar a matriz A-1.
![]()
Veja também: Teorema de Laplace — método eficiente para calcular o determinante de matrizes
Exemplo 2:
Determine a matriz inversa da matriz:
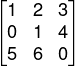
Utilizando o mesmo processo da matriz 2x2, temos que:
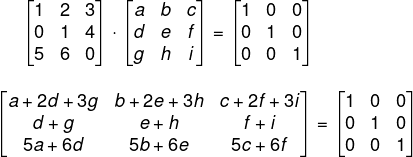
Vamos dividir o problema em três sistemas, um para cada coluna da matriz:
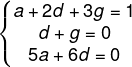
Pela segunda equação, temos que:
d+g=0 → g = – d
Pela terceira, temos que:
5a+6d = 0 → a = –6d/5
Pelo método da substituição, chegamos a:
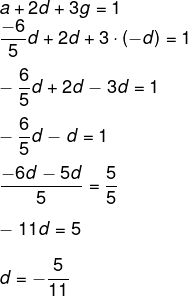
Conhecendo o valor de d, é possível encontrar o valor de a e g.
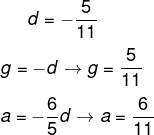
Agora vamos montar o segundo sistema e resolvê-lo utilizando o mesmo método:
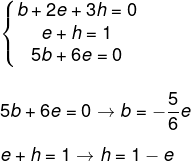
Substituindo na primeira equação, temos que:
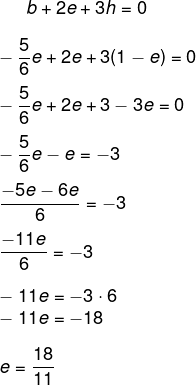
Tendo o valor de e, podemos encontrar o valor de b e h.
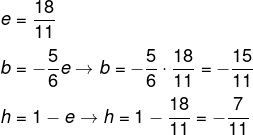
Por fim, vamos resolver o terceiro sistema:
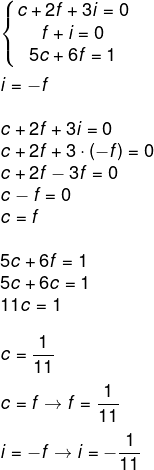
Agora que conhecemos o valor de todas as variáveis, podemos reescrever a inversa A-1:
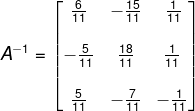
Propriedades da matriz inversa
A matriz inversa possui propriedades importantes.
-
A inversa da matriz inversa de B é igual à matriz B.
(B-1)-1 = B
-
Uma matriz só possuirá inversa se o seu determinante for diferente de zero. Caso o determinante det(B) seja igual a zero, a matriz não possui inversa.
-
A matriz transposta da matriz inversa é igual à matriz inversa da matriz transposta.
(B-1)t = (Bt)-1
-
A inversa de uma matriz identidade é sempre igual a ela mesma.
I-1 = I
-
A inversa do produto de duas matrizes é igual ao produto das inversas.
(A×B)-1 = B-1×A-1
Acesse também: Determinantes de matrizes de ordem 1, 2 e 3

Exercícios resolvidos
Questão 1 – Dada a matriz A, podemos afirmar que ela não será inversível se x for igual a:
![]()
A) x = 4
B) x = – 4
C) x = 2
D) x = – 2
E) x = 0
Resolução
Alternativa B.
Para que a matriz não seja inversível, o seu determinante tem que ser igual a 0. Então, temos que:
det(A) = – 2x – 8 ·1 = 0
– 2x – 8 = 0
– 2x = 8
x = 8 : (– 2)
x = – 4
Questão 2 – (UEMG adaptada ) Se A e B são inversas, então o valor de x é:
![]()
A) 5
B) 6
C) 7
D) 9
Resolução
Alternativa A.
Para que elas sejam inversas, o produto dessas matrizes é igual à matriz identidade:
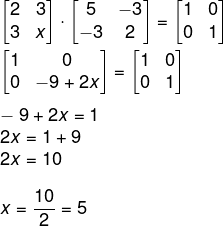
Artigos Relacionados

Últimas notícias
Outras matérias


















