Paralelepípedo

O paralelepípedo é um sólido geométrico presente no nosso dia a dia em vários objetos, como caixas, embalagens de remédio, tijolos, entre outros. Estudado na Geometria Espacial e composto por 6 faces, 8 vértices e 12 arestas, o paralelepípedo recebe esse nome por possuir faces formadas por paralelogramos, que são quadriláteros de lados paralelos, como o retângulo e o quadrado.
Veja também: Pirâmide — outro sólido geométrico estudado na Geometria Espacial
Resumo sobre paralelepípedo
- O paralelepípedo é um sólido geométrico que possui 6 faces, 8 vértices e 12 arestas.
- As faces do paralelepípedo são formadas por paralelogramos.
- O paralelepípedo pode ser reto ou oblíquo.
- O volume de um paralelepípedo qualquer é calculado pelo produto entre a área da base e a altura:
\(V=A_b\cdot h\)
- O volume do paralelepípedo reto considerando o comprimento, a largura e a altura é a multiplicação das medidas das três dimensões:
\(V=a\ \cdot b\ \cdot c\)
- O paralelepípedo oblíquo não possui fórmula específica para o cálculo da área total e da medida da sua diagonal. Já o paralelepípedo reto possui.
- A fórmula para calcular a área total de um paralelepípedo reto de dimensões a, b e c é:
\(A_T=2ab+2ac+2bc\)
- Já o comprimento da diagonal do paralelepípedo reto é calculado pela fórmula:
\(d=\sqrt{a^2+b^2+c^2}\)
Quais são os elementos do paralelepípedo?
Como todos os sólidos geométricos, os principais elementos do paralelepípedo são as faces, os vértices e as arestas. O paralelepípedo é composto por 6 faces, 8 vértices e 12 arestas.
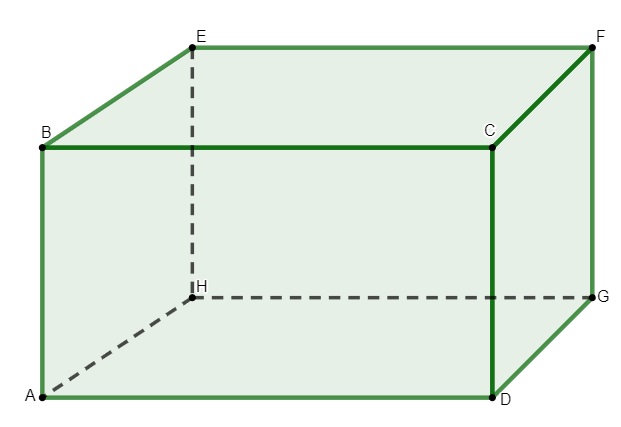
- Faces: são os paralelogramos
ABCD, CDGF, ABEG, ADGH, EFGH, BCFE
- Vértices: são os pontos
A, B, C, D, E, F, G, H
- Arestas: são os segmentos de reta que ligam o vértice, representados por
\(\overline{AB},\overline{BC},\overline{CD},\overline{AD},\overline{AH},\overline{EH},\overline{BE},\overline{EF},\overline{FC},\overline{GH},\overline{FG},\overline{DG}\)
Classificação do paralelepípedo
Podemos classificar os paralelepípedos dependendo da inclinação das suas arestas laterais com a sua base. O paralelepípedo pode ser considerado reto ou oblíquo.
O paralelepípedo é reto se a sua aresta lateral for perpendicular à base, ou seja, formar um ângulo reto (ângulo de 90°) com a sua base. Caso contrário, ele é classificado como oblíquo, ou seja, se a inclinação da aresta com a base for diferente de 90°, o paralelepípedo será oblíquo.
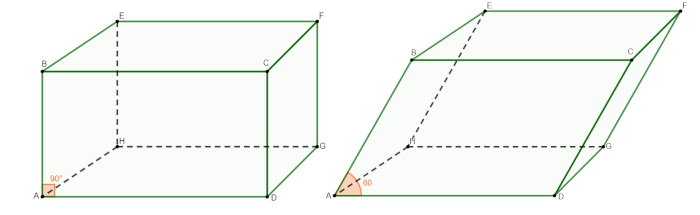
Na imagem, podemos perceber que no primeiro paralelepípedo o ângulo entre a aresta lateral e a base é de 90°, logo esse paralelepípedo é reto. Entretanto, no segundo paralelepípedo, há um ângulo de 60° com a base, o que faz com que o segundo paralelepípedo seja oblíquo.
Fórmulas do paralelepípedo
Podemos calcular o volume, a área total e a diagonal de um paralelepípedo. Veja a seguir.
→ Volume do paralelepípedo
O paralelepípedo é considerado um prisma. Prismas são sólidos geométricos que possuem sempre duas bases congruentes formadas por polígonos e arestas laterais ligando essas bases. De modo geral, o volume de um paralelepípedo qualquer, ou seja, tanto reto como oblíquo, é calculado como o volume de todos os prismas.
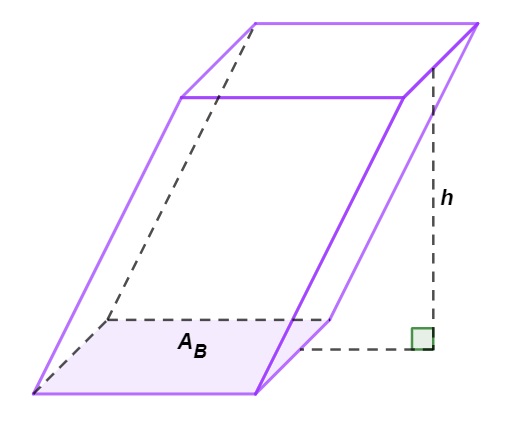
Como a fórmula de cálculo do volume é a mesma para todo prisma, temos que:
\(V=A_b\cdot h\)
Importante: Essa fórmula do volume é para qualquer tipo de paralelepípedo, mas existe uma fórmula específica para o paralelepípedo reto considerando seu comprimento, sua largura e sua altura que será apresentada a seguir.
→ Volume do paralelepípedo reto
Como a base de um paralelepípedo reto é um retângulo, para calcular a área da base multiplicamos o comprimento pela largura, ou seja, multiplicamos as duas dimensões do retângulo. Então, para calcular o volume de um paralelepípedo reto, basta multiplicar comprimento, largura e altura.
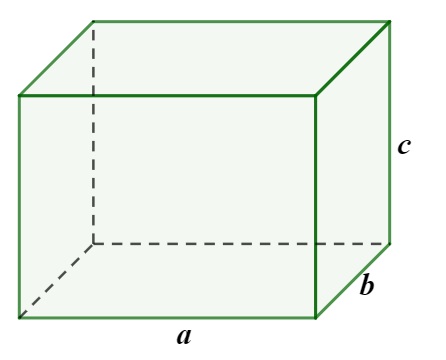
A fórmula de cálculo do volume do paralelepípedo reto é
\(V=a\cdot b\cdot c\)
Importante: O paralelepípedo oblíquo não possui fórmulas específicas para o cálculo de sua área e de sua diagonal, mas o paralelepípedo reto possui.
→ Área do paralelepípedo
Considerando o paralelepípedo reto com dimensões medindo a, b e c, a área ou área total de um sólido é a soma das áreas das suas faces.
No paralelepípedo, as faces opostas são congruentes. Logo, as faces possuem a mesma área de duas a duas. A área de cada face é a multiplicação da sua largura pelo seu comprimento, então podemos calcular essa área total pela fórmula:
\(A_T=2(ab+ac+bc)\)
→ Diagonal do paralelepípedo
A diagonal é o segmento de reta que liga dois vértices opostos do paralelepípedo, como na imagem a seguir:
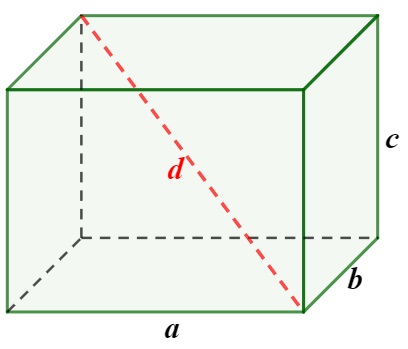
Para calcular o comprimento da diagonal, utilizamos a fórmula:
\(d=\sqrt{a^2+b^2+c^2}\)
Saiba mais: Como pode ser obtido o número de diagonais de um polígono?
Exercícios resolvidos sobre paralelepípedo
Um container possui formato de um paralelepípedo reto, com medidas internas de 5,8 metros de comprimento, 2,3 metros de largura e 2,6 metros de altura. Então o volume desse container é de, aproximadamente:
A) 35,0 m³
B) 34,7 m³
C) 33,9 m³
D) 32,8 m³
E) 31,4 m³
Resolução:
Alternativa B
Calculando o volume:
\(V=5,8\cdot2,3\cdot2,6\)
\(V=34,684{\ m}^3\)
O volume é de aproximadamente 34,7 m³.
Questão 2
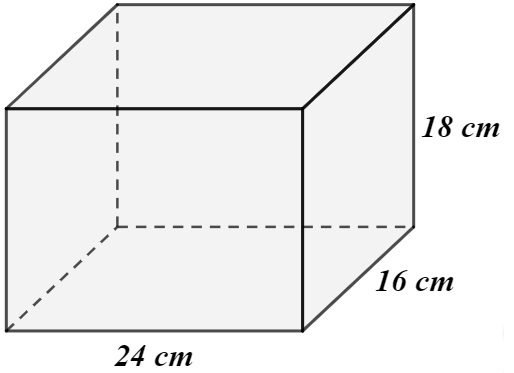
A medida da diagonal do paralelepípedo a seguir é de, aproximadamente:
A) 30 cm
B) 31 cm
C) 32 cm
D) 34 cm
E) 35 cm
Resolução:
Alternativa D
Calculando a diagonal, temos que:
\(d=\sqrt{{24}^2+{16}^2+{18}^2}\)
\(d=\sqrt{576+256+324}\)
\(d=\sqrt{1156}\)
\(d=34\)
Artigos Relacionados

Últimas notícias
Outras matérias


















