Permutação simples
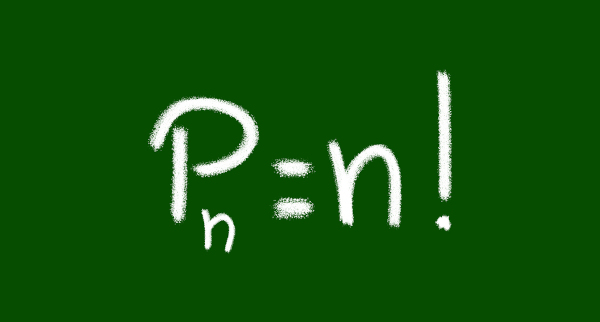
A permutação simples é um tipo de agrupamento estudado na análise combinatória. Permutar os elementos de um conjunto nada mais é que formar agrupamentos ordenados com todos os elementos desse conjunto. Representamos a permutação de n elementos por Pn. Para calcular a permutação de um conjunto com n elementos todos distintos, basta calcular o valor do fatorial desses n elementos, ou seja, Pn = n!.
Além da permutação simples, conhecemos também a permutação com repetição, que é quando temos dois elementos ou mais repetidos no conjunto. Para calcular a permutação com repetições, utilizamos uma fórmula específica.
Leia também: Arranjo simples – outro importante tipo de agrupamento estudado na análise combinatória
Resumo sobre permutação simples
-
A permutação simples é um tipo de agrupamento estudado na análise combinatória.
-
Representamos a permutação de n elementos por Pn.
-
Para calcular a permutação simples de n elementos, utilizamos a fórmula Pn = n!.
O que é uma permutação simples?
Dado um conjunto com n elementos todos distintos entre si, conhecemos como permutação simples de n elementos todos os agrupamentos ordenados que podemos formar utilizando todos os elementos desse conjunto.
Exemplo 1:
Dado o conjunto de letras {A, B, C}, podemos listar todas as permutações possíveis desse conjunto:
(A, B, C); (A, C, B); (B, A, C); (B, C, A); (C, A, B); (C, B, A).
Note que existem 6 permutações possíveis para esses 3 elementos.
Exemplo 2:
Listaremos todos os números que podemos escrever com os algarismos 1, 2, 3 e 4, são eles:
(1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321)
Note agora que existem 24 permutações possíveis formadas com 4 elementos. Quanto maior a quantidade de elementos, maior será o número de permutações possíveis.
Fórmula da permutação simples
Muitas vezes em problemas envolvendo permutação, o nosso interesse não está em listar os agrupamentos, mas sim em calcular a quantidade de agrupamentos possíveis. Para encontrar essa quantidade de permutações possíveis, sem a necessidade de listar e contar esses agrupamentos, utilizamos a fórmula da permutação.
Para calcular a permutação simples de n elementos representada por Pn, utilizamos a fórmula:
|
Pn = n! |
Veja também: Quais são os critérios para identificação de arranjo ou combinação?
Como calcular a permutação simples?
Para calcular a permutação simples, é necessário identificar quantos elementos estamos permutando e também calcular o fatorial desse número. Calcular o fatorial de um número nada mais é que multiplicá-lo por todos os seus antecessores maiores que 0.
Exemplo:
Calcule todas as permutações que podemos formar com 5 elementos.
Para calcular a permutação de 5 elementos, basta calcular 5!
P5 = 5!
Para calcular 5!, basta multiplicar 5 por seus antecessores:
P5 = 5 · 4 · 3 · 2 · 1
P5 = 120
Então, o número de permutações possíveis que podemos formar com 5 elementos é 120.
Permutação com repetições
Existem casos particulares de permutação em que há elementos repetidos no conjunto, por exemplo, na formação de anagramas de palavras que possuem pelo menos duas letras repetidas.
Para calcular a permutação com repetição, utilizamos a fórmula:
![]()
n → quantidade de elementos no conjunto
k1, k2, … kn → quantidade de vezes que um mesmo elemento se repetiu
Exemplo:
Quantos são os anagramas que podemos formar com o nome ARARA?
Note que há 5 elementos, porém a letra R se repete 2 vezes e a letra A se repete 3 vezes. Então, temos que:
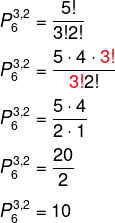
-
Videoaula sobre permutação simples e permutação com repetição
Exercícios resolvidos
Questão 1 - De quantas maneiras distintas 6 amigos podem escolher os seus lugares em uma sala de cinema, sabendo que todas as 6 cadeiras estão dispostas em uma fila?
A) 6
B) 12
C) 36
D) 120
E) 720
Resolução
Alternativa E
Vamos calcular uma permutação de 6 elementos:
P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Questão 2 - (Fatec - SP) Uma pessoa dispõe de 4 discos diferentes de MPB, 4 discos diferentes de rock e 2 discos diferentes de música clássica. O número de modos distintos como essa pessoa pode organizá-los em uma estante, de tal forma que discos do mesmo gênero estejam sempre juntos e os de rock sempre na mesma ordem, é:
A) 144
B) 1152
C) 48
D) 50
E) 288
Resolução
Alternativa E
Podemos separar esse problema entre as permutações que podem ser feitas.
Primeiro podemos permutar os gêneros músicas, escolhendo a ordem entre MPB, rock e música clássica, ou seja, permutação de 3 elementos, P3.
Além da permutação entre os estilos musicais, podemos permutar os discos de um mesmo gênero. Entre os discos de MPB, há 4 opções, ou seja, P4, e entre os discos de música clássica, P2. Não podemos permutar os discos de rock, que já possuem ordem definida.
Escolheremos, então, a ordem dos estilos musicais, a ordem dos discos de MPB e a ordem dos discos de música clássica. Pelo princípio multiplicativo, basta multiplicar as permutações.
Seja N o número de ordens possíveis, temos que:
N = P3 · P4 · P2
N = 3! · 4! · 2!
N = (3 · 2 · 1) · (4 · 3 · 2 · 1) · (2 · 1)
N = 6 · 24 · 2
N = 288
Artigos Relacionados

Últimas notícias
Outras matérias


















