Pontos notáveis de um triângulo

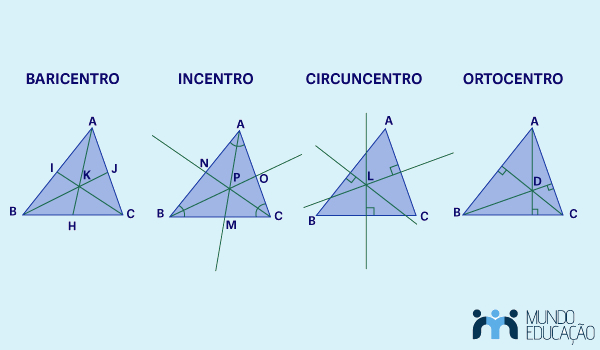
Os pontos notáveis de um triângulo são os pontos de encontro de retas, semirretas ou segmentos específicos desenhados em um triângulo. Esses pontos estão relacionados aos vértices, lados e ângulos do triângulo. Existem quatro pontos notáveis de um triângulo:

• baricentro;
• incentro;
• circuncentro;
• ortocentro.

Leia também: O que é e quando ocorre congruência entre triângulos?

Resumo sobre os pontos notáveis de um triângulo

• Os pontos notáveis de um triângulo são interseções de retas, semirretas ou segmentos especiais traçados no triângulo.
• Baricentro, incentro, circuncentro e ortocentro são os pontos notáveis de um triângulo.
• O baricentro é o ponto de encontro das medianas, segmentos que unem cada vértice ao ponto médio do lado oposto.
• O incentro é o ponto de encontro das bissetrizes, semirretas que dividem cada ângulo em dois ângulos congruentes. Esse ponto também é o centro da circunferência inscrita no triângulo.
• O circuncentro é o ponto de encontro das mediatrizes, retas perpendiculares a cada lado do triângulo e que cruzam o ponto médio.
• O ortocentro é o ponto de encontro das alturas, segmentos perpendiculares a cada lado com uma extremidade no vértice oposto.

O que são pontos notáveis de um triângulo?

Os pontos notáveis de um triângulo são os pontos de encontro de retas, de semirretas ou de segmentos específicos desenhados em um triângulo.

Quais são os pontos notáveis de um triângulo?

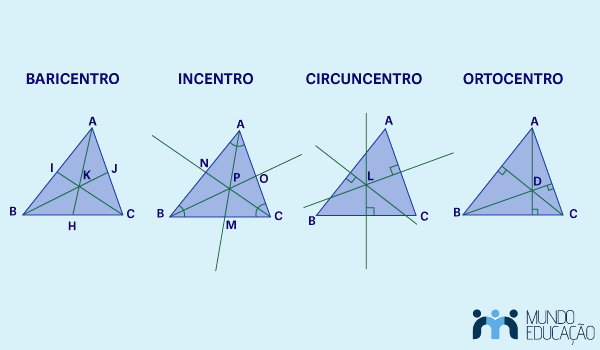
Existem quatro pontos notáveis de um triângulo: baricentro, incentro, circuncentro e ortocentro. Esses pontos são obtidos, respectivamente, a partir das medianas, bissetrizes, mediatrizes e alturas de um triângulo.

Como diferenciar os pontos notáveis de um triângulo?

Para diferenciar os pontos notáveis de um triângulo, devemos saber os conceitos de mediana, bissetriz, mediatriz e altura. Considerando cada um desses objetos, podemos caracterizar os pontos notáveis.

→ Baricentro

O baricentro é a interseção das medianas de um triângulo.

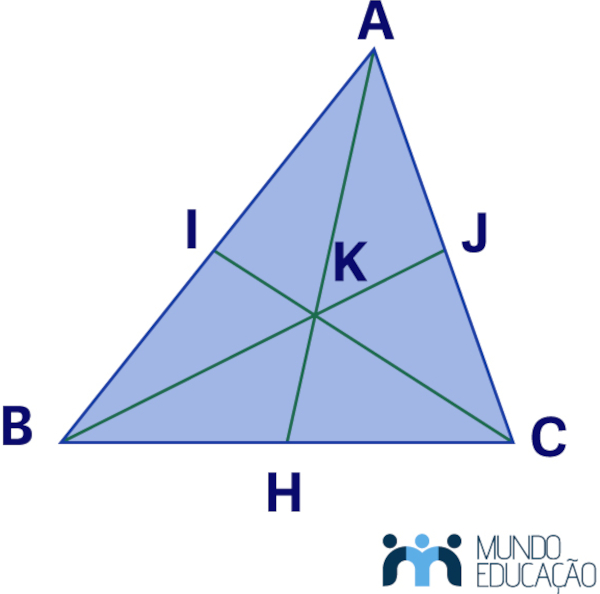
Uma propriedade importante do baricentro é que ele divide cada mediana na proporção 2:1. No triângulo ABC, por exemplo, o segmento AK tem o dobro da medida do segmento HK.

Saiba mais detalhes sobre o baricentro de um triângulo clicando aqui.

→ Incentro

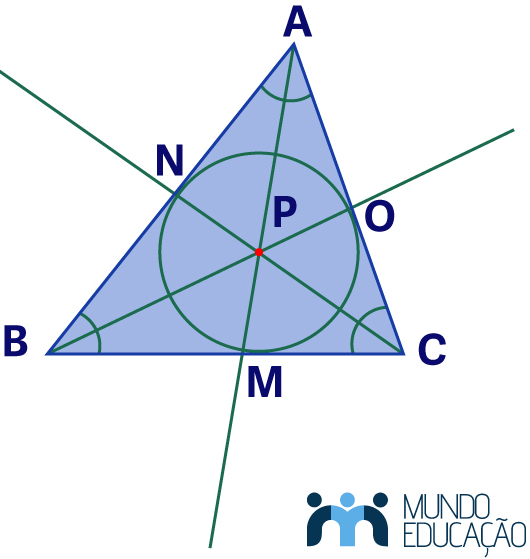
O incentro é a interseção das bissetrizes de um triângulo.

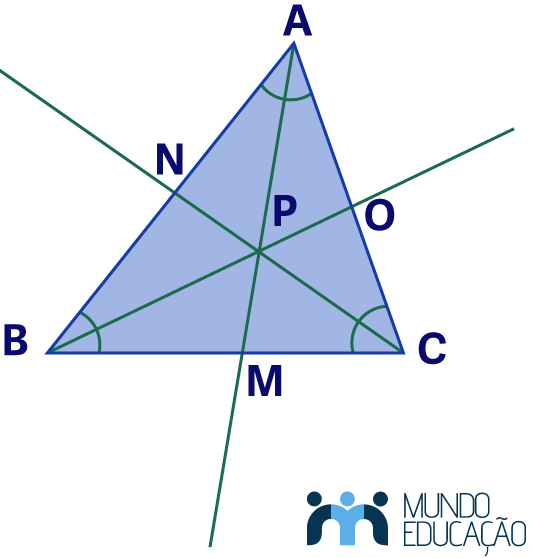
Uma propriedade importante do incentro é que ele é o centro da circunferência inscrita no triângulo, ou seja, a circunferência que tangencia cada um dos lados do triângulo.

→ Circuncentro

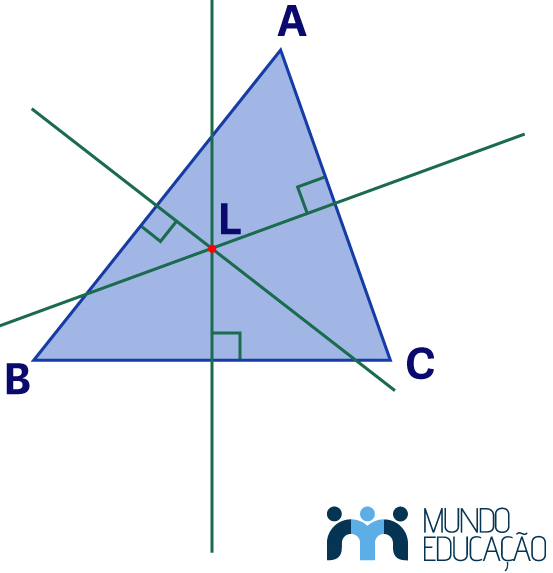
O circuncentro é a interseção das mediatrizes de um triângulo.

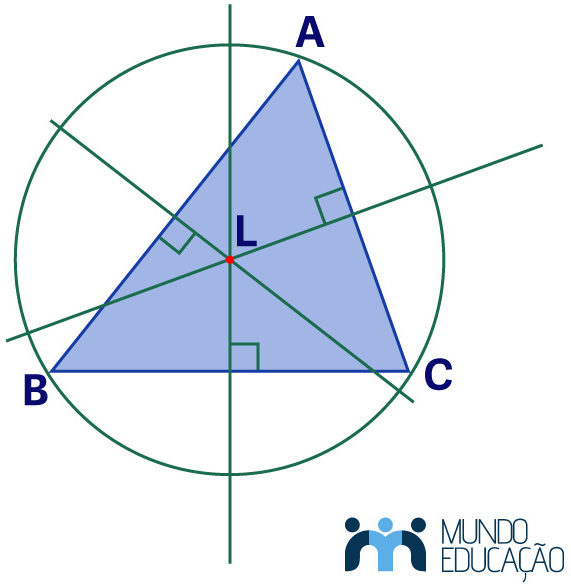
Uma propriedade importante do circuncentro é que ele é o centro da circunferência circunscrita no triângulo, ou seja, a circunferência que contém os vértices do triângulo.

→ Ortocentro

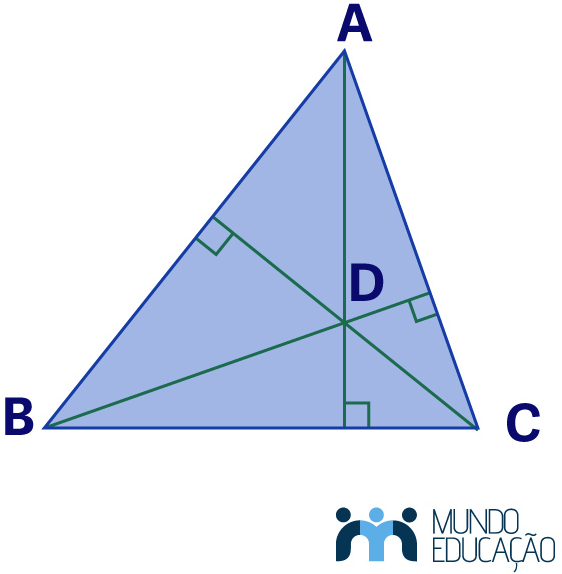
O ortocentro é a interseção das alturas de um triângulo.

Pontos notáveis de um triângulo isósceles

Em um triângulo isósceles, os quatro pontos notáveis estão sobre o mesmo segmento. Considere um triângulo isósceles com dois lados de medida x e um lado de medida y. Nesse triângulo, a mediana, a bissetriz, a mediatriz e a altura relativas ao lado de medida y são coincidentes. Assim, os quatro pontos notáveis do triângulo isósceles ABC estão sobre o segmento AH.

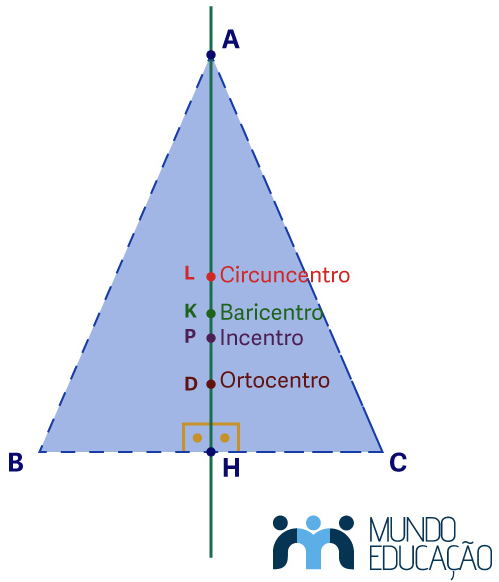
Pontos notáveis de um triângulo equilátero

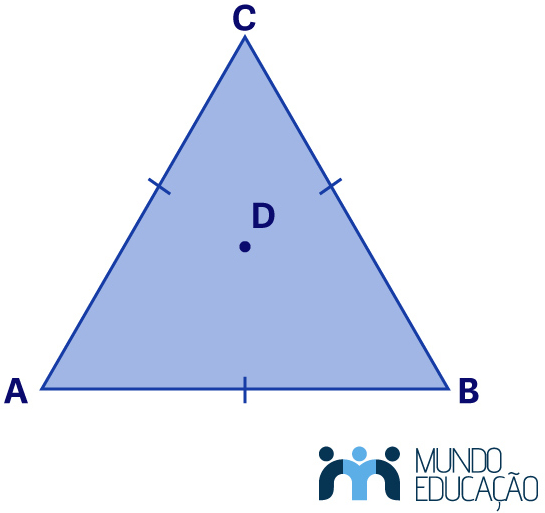
Em um triângulo equilátero, cujos três lados têm a mesma medida, os quatro pontos notáveis são coincidentes. No triângulo equilátero ABC abaixo, o ponto D é o baricentro, incentro, circuncentro e ortocentro:

Altura, mediana, bissetriz e mediatriz de um triângulo

→ Mediana de um triângulo

A mediana de um triângulo é um segmento com extremidades no vértice e no ponto médio do lado oposto.

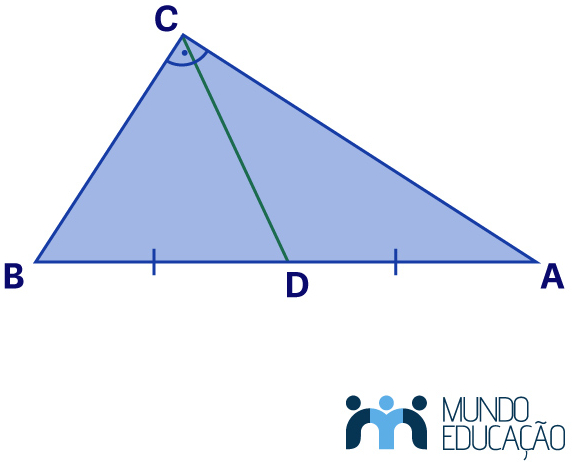
Note que um triângulo tem três medianas, pois esse polígono tem três vértices e três lados.

→ Bissetriz de um triângulo

A bissetriz de um triângulo é uma semirreta com extremidade no vértice e que divide o ângulo do triângulo em ângulos congruentes.

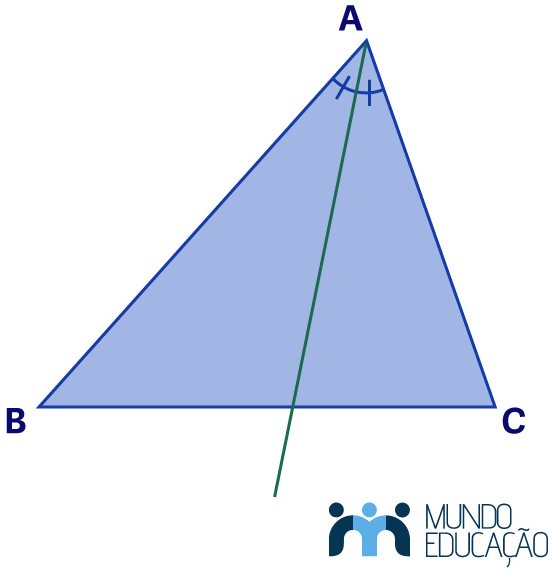
Note que um triângulo tem três bissetrizes, pois esse polígono tem três ângulos.

Saiba mais detalhes sobre a bissetriz clicando aqui.

→ Mediatriz de um triângulo

A mediatriz de um triângulo é uma reta perpendicular a um lado que cruza seu ponto médio.

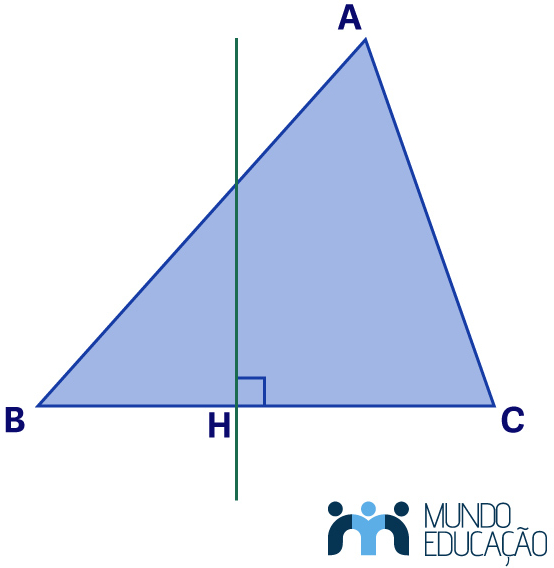
Note que um triângulo tem três mediatrizes, pois esse polígono tem três lados.

Saiba mais detalhes sobre a mediatriz clicando aqui.

→ Altura de um triângulo

A altura de um triângulo é um segmento perpendicular a um lado com extremidade no vértice oposto.

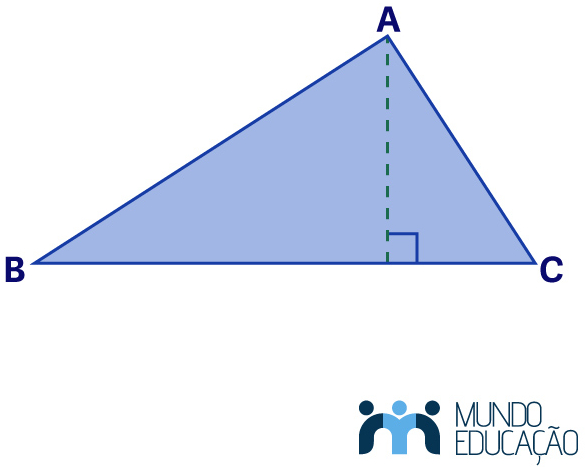
Note que um triângulo tem três alturas, pois esse polígono tem três vértices e três lados.

Importante: Um segmento que conecta um vértice de um triângulo ao lado oposto é chamado de ceviana. As medianas e alturas de um triângulo são casos particulares de ceviana.

Exercícios resolvidos sobre pontos notáveis de um triângulo

Questão 1

Os pontos de encontro das mediatrizes e das medianas de um triângulo são chamados, respectivamente, de

A) incentro e baricentro.

B) baricentro e ortocentro.

C) ortocentro e circuncentro.

D) circuncentro e baricentro.

Resolução:

Alternativa D

O circuncentro é a interseção das mediatrizes de um triângulo e o baricentro é a interseção das medianas de um triângulo.

Questão 2

Em uma praça com o formato de um triângulo escaleno, será posicionado um bebedouro no ponto equidistante dos lados. O bebedouro deve ser posicionado em qual ponto do triângulo que delimita a região da praça?

A) Incentro

B) Baricentro

C) Ortocentro

D) Circuncentro

Resolução:

Alternativa A

Como incentro é o centro da circunferência inscrita no triângulo, esse ponto é equidistante dos lados do triângulo.

Fontes

MACHADO, P.F. Fundamentos de geometria plana. Belo horizonte: CAED-UFMG, 2012.

REZENDE, E. Q. F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.