Potenciação de frações algébricas
Frações algébricas são expressões que possuem pelo menos uma incógnita no denominador. São exemplos de frações algébricas:
1
x
k2x3y4z
abc
Suponha que as frações acima sejam elevadas ao quadrado. Essa potência será representada da seguinte maneira:
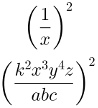
Cálculo de potenciação de frações algébricas
A primeira propriedade que deve ser usada na potenciação de fração algébrica é a de potência de fração. Essa propriedade garante que potências desse tipo podem ser feitas para o numerador e para o denominador separadamente.
A propriedade a que nos referimos é a seguinte:
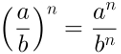
Como exemplo, vamos calcular a potência de fração algébrica a seguir:
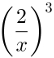
Aplicando a propriedade acima e realizando os cálculos obtidos, teremos:
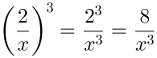
Também é possível que seja necessário usar a propriedade de potência de produto. Quando um produto de números (ou incógnitas) diferentes está todo elevado a algum expoente, cada um dos fatores desse produto deve ser elevado separadamente. Matematicamente:
![]()
Vamos resolver a potência de fração algébrica a seguir:
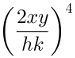
A solução desse exemplo é a seguinte:
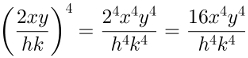
A terceira propriedade usada nesses cálculos é a “potência de potência”. Se houver uma potência elevada a algum expoente, multiplicaremos os dois expoentes.
A última propriedade é a de divisão de potências de mesma base, na qual mantemos a base e subtraímos os expoentes. Essa propriedade é usada para simplificar frações algébricas. Veja um exemplo:
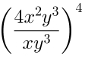
Aplicando as quatro propriedades discutidas anteriormente, teremos:
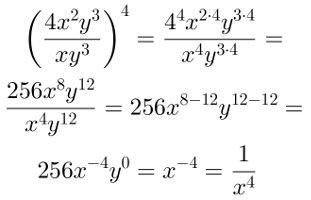
Artigos Relacionados

Últimas notícias
Outras matérias


















